Image0082 BMP

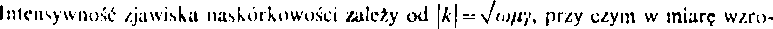
stu k naskórkowość staje się silniejsza. Wobec tego naskórkowość zwiększa się w miarę wzrostu częstotliwości prądu oraz przenikalności magnetycznej i konduktywno.śd przewodu. Z tego powodu zjawisko naskórkowości zaznacza się silnie przy dużych częstotliwościach i w przypadku materiałów dobrze przewodzących. Naskórkowość zależy również od rozmiarów poprzecznych, przewodu i jest silniejsza w przewodach grubych,

9.2.3. Rezystancja i mdukcyjność wewnętrzna

Impedancję wewnętrzną odcinka przewodu o długości I obliczymy na podstawie wzoru

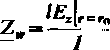
(9.20)

wynikającego z zależności (8.56). Podstawiając E, z wyrażenia (9.17), otrzymujemy

-^w nr^y 2 I,(kr₀)

(9.21)

l

Wielkość 2 zawarta w Lym wzorze jest rezystancją odcinka przewodu przy przepły

wie prądu stałego.

Wzór (9.21) można również otrzymać, obliczając strumień zespolonego wektora Poyntinga przez powierzchnię boczną przewodu, który jest równy na podstawie twierdzenia Poyntinga (por. p. 8,3) mocy zespolonej związanej z obszarem wewnętrznym przewodu, oraz wykorzystując wzór S = Z_wi², gdzie i jest wartością skuteczną prądu w przewodzie.

Zmodyfikowane funkcje Iśessela występujące we wzorze (9.21) przybierają wartości zespolone; funkcje te przedstawimy w postaci

Io(kr₀) = b₀c^ll!°,

h (*r<_ł) = *_Ie^w,>

(9.22)

przy czym zarówno moduły b₀, 6, jak i argumenty f₀, fi, są funkcjami |fc| r_a. Po podstawieniu tych wyrażeń do zależności (9.21) i po wyodrębnieniu części rzeczywistej i urojonej, otrzymujemy wzory określające rezystancję i reaktancję wewnętrzną

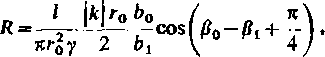
(9.23)

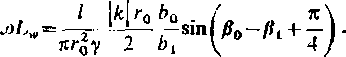
(9-24)

Obecnie obliczymy rezystancję i indukcyjność wewnętrzną przewodu przy małych /ęsiotliwośeiach, gdy |A[ r„«l. W rozwinięciach zmodyfikowanych funkcji Uessela

wobec czego

^o(z)wl +— » 4

/i<*)*

K>

k.²r² l\ ^r°

ip(kr₀)^ 2__4^

h(kr₀)~kr_{Q 1 +} k*r% ⁺ 8

Wykorzystując wzór przybliżony

l + x

il-x

prawdziwy dla |jrj«l, po pominięciu wyrazu zawierającego k*Ą, otrzymujemy

/,(*r₀) *r₀\    4 J\ 8 } kr₀\ 8 )

wobec czego na podstawie zależyości (9.21) mamy

z.-4(r₊^).

nr₀y\ 8 )

skąd po podstawieniu /c^ł=j<upy i po wyodrębnieniu części rzeczywistej i urojonej, znajdujemy

R',

/

nr%y

L

^w 8ji

W wyniku otrzymaliśmy rezystancję przewodu dla prądu stałego, a wzór dla induk-eyjności wewnętrznej ma taką samą postać jak wyprowadzone w p. 6.5.2 wyrażenie przy założeniu, że rozkład prądu w przekroju poprzecznym przewodu jest równomierny.

Tabela 9.1

/	R 1 nrof	Łitt z Sn
10*	1,00	1,00
10^s	1.01	0,991
io< ; i,yi		0,718