Image0042 BMP

Wobec C/CgO

grad,,

r

gdzie (por. rys. 4.9):

r= U*-*') +1 „( y - y) +1,(= - Z) ■

W wyniku mamy zatem

rotp

dl rxdl dlxr

r

,3

wobec czego

r

r

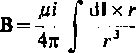
c

(4.38)

zgodnie ze wzorem (4.36). Natężenie pola magnetycznego wytworzone w punkcie P przez prąd i płynący w przewodzie C wynosi

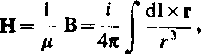
c

(4.39)

zaś natężenie pola magnetycznego wytworzone w punkcie P przez prąd i płynący w odcinku elementarnym dl przewodu wyraża się wzorem a jego miarą jest gdzie: a jest kątem między wektorem r a wektorem dl (rys. 4.9).

Wzory (4.39) — (4.41) przedstawiają prawo Biota-Savarta, które pozwala wyznaczyć natężenie pola magnetycznego w otoczeniu przewodów przewodzących prądy. Zastosowanie prawa Biota-Savarla ilustrują przykłady.

i

P

a

i

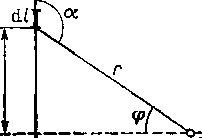
Rys. 4.10. Przewód prostoliniowy przewodzący prąd

Inku przykład obliczymy natężenie pulu magnetycznego wyiwornmr w punkcie P I '/••/ ptąd i płynący u bardzo długim pt/ewuil/ic prostoliniowym znajdującym się w sro-.!. >Msku jednorodnym (rys. 4,10). Natężenie pola magnetycznego w punkcie /'jest pro-• t. 1'intłc do płaszczyzny przechodzącej przez len punkt i oś przewodu. Na podstawie

a    a

i -    4 Id mamy x = 90 Ytp, r— — -, I=algq>, czyli d/=    , d<p. Podstawiając po-

cos <p    cos ę

wyrażenia do wzoru (4.41), znajdujemy

i

dH = — cos tpdip. 4 na

Wektor dH jest prostopadły do płaszczyzny rysunku, niezależnie od położenia elementu • ii, wobec czego    ⁹

I./2

cos (od(s =

i

2 na

-njl

(>tiz\maliśmy taki sam wynik, jak w p. 4.2.1 przy zastosowaniu prawa przepływu.

4.4.2. Natężenie pola magnetycznego na osi pierścienia

l’i ;|d i płynie w pierścieniu o promieniu r₀ (rys. 4.11). Obliczymy natężenie pola magnet yc/.ncgo w punkcie P położonym na osi pierścienia.

Natężenie pola magnetycznego wytworzone przez element pierścienia o długości dl

w ynosi

_J i di

d«=--₂ 4tt r

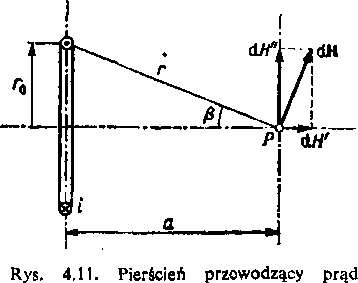
zgodnie ze wzorem (4.41), ponieważ kąt a między dowolnym elementem dl a odcinkiem r i< I zawsze równy 90°.

Wektor dH rozkładamy na składową dli' styczną do osi pierścienia oraz na składową <!//'' normalną do tej osi. Składowe normalne pochodzące od dwóch elementów dl położonych przeciwległe na obwodzie pierścienia znoszą się, wobec czego wektor H natężenia

polu magnetycznego wytworzonego przez prąd w całym pierścieniu ma kierunek jego osi.