Image0069 BMP

1

gdzie

(7.9)

W dalszych przekształceniach wykorzystujemy tożsamość wektorową (por. p. 1,2.4)|

rot rot A = grad div A - V² A, a w celu uproszczenia równania, przyjmujemy

i ev

div A = — , —.    (7.10)

v 8t

Przyjęcie tego warunku jest dopuszczalne ze względu na niejednoznaczność określenia potencjału wektorowego za pomocą wzoru (7.5), jak to wynika z rozważań podanych w p. 4.3.2.

W wyniku przekształceń otrzymujemy równanie różniczkowe dla potencjału wektorowego

V²A-

1 5²A

vⁱ 8t²ⁱ

= -ftJ

(7.11)

będące niejednorodnym równaniem Falowym.

W układzie współrzędnych prostokątnych równanie wektorowe (7.11) jest rówaoważne trzem równaniom skalarnym dla poszczególnych składowych:

V ²A_i-

vu_y-

v²a_i~

1	8^2Ax
V	dl^2 ~
1	d^2Ar
V	di^2	-PJ,>
1	8^2Az
~2	8t^z "	-HJt.

(7.12)

Równanie różniczkowe dla potencjału skalarnego znajdujemy na podstawie równania (7.3). Podstawiając wyrażenie (7.6) do tego równania, otrzymujemy

8    , p

- divA-V²lA=, ot    e

bowiem divgrad V=V²V. Przy uwzględnieniu zależności (7.10), otrzymujemy w wyniku

V²

;i 8²V

■v² 8t²

P_

e

(7.13)

Stwierdzamy zatem, że potencjał skalarny pola elektromagnetycznego spełnia niejednorodne równanie Falowe.

7.2. Falowy charakter pola elektromagnetycznego

W punkcie 7.1.2 udowodniliśmy, że potencjały elektrodynamiczne spełniają niejednorodne równania falowe

1 3^2V o _____
p^2 3t^2 e ’	(7.14)
1 8^2A
7 a?	(7.15)
i V=1-r. \>ep	(7.16)
	4

gdzie:

Równania te są spełnione w każdym punkcie obszaru v, w którym istnieje ładunek przestrzenny o gęstości p oraz płynie prąd o gęstości J.

Załóżmy, że na zewnątrz obszaru o nie ma ani ładunku przestrzennego, ani przepływu prądu, wobec czego p=0 oraz J=0. W łych warunkach otrzymuje się jednorodne równania falowe

V²K-

(7.17)

i o²v

-_T—v=0,

u² et²

V²A—

1 d²A

V ^_0,

(7.18)

spełnione na zewnątrz obszaru v.

Z matematyki wiadomo, że rozwiązanie równania falowego, tak jednorodnego jak i niejednorodnego przedstawia falę rozprzestrzeniającą się w środowisku z prędkością v. Oznacza to, że potencjały elektrodynamiczne mają charakter falowy. Ponieważ potencjały te określają wektory E, H, więc również wektory charakteryzujące pole elektromagnetyczne mają charakter falowy. Na tej podstawie wnioskujemy, że pole elektro magnetyczne ma strukturę falową.

Można udowodnić, że podstawowe rozwiązania równań (7.14), (7.15), (7.17) i (7.18) wyrażają się wzorami:

V(P,ł)=

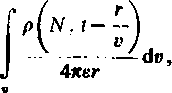
A (P,t) =

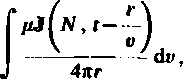
V

<(7-19)

(7.20) przedstawiającymi potencjały elektrodynamiczne w punkcie obserwacji P. W tych wyrażeniach A"jest punktem źródłowym, r — odległością punktu obserwacji od punktu źródłowego (rys. 7.1), zaś całkowanie wykonywane jest względem współrzędnych punktu źródłowego. Potencjały V(P, t) oraz A (P, f) spełniają odpowiednio niejednorodne równania falowe we wnętrzu obszaru i>, a równania jednorodne - na zewnątrz tego obszaru.