Image0093 BMP

Eliminując E, t. równań (9.103) i (9.104), otrzymujemy równanie Bessclu

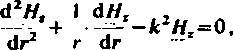
(9.105)

gdzie: k określone jest wzorem (9.85).

Równanie (9.105) spełnione jest we wnętrzu walca, a jego rozwiązaniem jest

Ił_tl=sA_ll^kr) + A_rK₀(kr), 0 śrśr₀,

gdzie: /„(«) oraz K₀(u) są zmodyfikowanymi funkcjami Bessela rzędu zerowego, pierwszego i drugiego rodzaju. Biorąc pod uwagę, że rozwiązanie powinno być skończone dla r—0, przyjmujemy A₂—0; mamy zatem

(9.106)

Na zewnątrz walca spełnione jest równanie (9.105) dla k-0 przy założeniu, te środowisko otaczające jest nieprzewodzące; otrzymuje się więc równanie Eulera

ó²H_i d H. _A

^rd^⁺dT⁼⁰’    ⁽⁹¹⁰⁷⁾

a jego rozwiązaniem jest

H,2 = A₃+A_A\nr_t    r>r₀.

Ponieważ wyrażenie to powinno przybierać wartości skończone przy r-»oo, bowiem gdy r-Kffl, więc ^4 = 0, wobec czego

(9.108)

Hz₂ — Ay—H₀,    > r o.

Warunek brzegowy dotyczący ciągłości składowej stycznej natężenia pola magnetycznego w punktach powierzchni granicznej przybiera postać

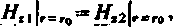
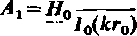
Wobec tego natężenie pola magnetycznego wyraża się wzorem

(9.109)

Natężenie pola elektrycznego obliczamy ze wzoru (9.103); otrzymujemy

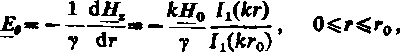
(9.110)

jowiem

dz

W celu obliczeniu strat wiropniowych wyznaczymy wektor Poyntingn na powierzchni walca; mamy

(E x H*),«* -(£, HtU", ■ 1* x l_t=(£, //*)_r._r„ I,.

a po podstawieniu zależności (9.109) i (9.110), otrzymujemy

(ĘxHV^=

7 ~Iotkr_or ^r ’

co dowodzi, że strumień mocy zespolonej wnika do wnętrza walca przez jego powierzchnię.

Zgodnie z twierdzeniem Poyntinga w postaci zespolonej, moc zespolona związana 7 obszarem wewnętrznym odcinka walca o długości / jest równa strumieniowi mocy zespo- , lonej wnikającemu przez granicę tego obszaru, czyli

UĄljfJcro) y Jo(^fcro)

Straty wiroprądowe P w odcinku walca o długości / są równe części rzeczywistej mocy zespolonej S. Przedstawiając funkcje Bessela /, oraz /₀ jak we wzorze (9.22), otrzymu

jemy

P-2vt₀IH%

Itop ń_Ł

--(

y ho

■cosj^! » \

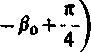
(9.111)

‘>.8. Straty wiroprądowe wywołane przez prądy w przewodach

9.8.1. Zależności podstawowe    _

Rozpatrzymy układ zawierający baTdzo długie i bardzo cienkie przewody 1,2, ...,« przewodzące prądy Ą,/₂    umieszczone w środowisku nieprzewodzącyra równo

legle do powierzchni granicznej półnieskończonej ściany metalowej (rys. 9.14). W ścianie metalowej indukują się prądy wirowe wskutek zmian czasowych pola magnetycznego wytworzonego przez prądy w przewodach. Celem naszych rozważań jest obliczenie strat

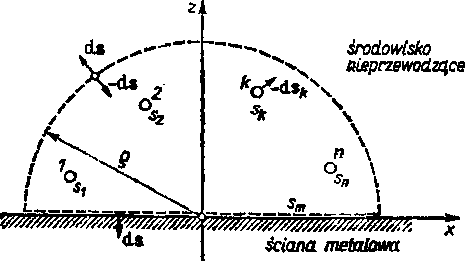
Rys. 9.14. Przewody równolegle /, 2,.... n nad powierzchnią półnieskończonej ściany metalowej