Image0071 BMP

Rozwiązaniem tego równaniu jest niezależna od czasu funkcja l'---a;+b, gdzie a oraz b si} stałymi. Otrzymana w ten sposób wielkość V nie ma jednak struktury falowej, wskutek czego nalepy przyjąć V~0. Widzimy zatem, że potencjał skalarny omawianego pola jest równy zeru.

Ma podstawie wzoru (7.6) stwierdzamy, że natężenie pola elektrycznego ma tylko jedną składową

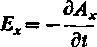
Natężenie pola magnetycznego obliczamy z zależności H = - rot A; znajdujemy stąd, że natężenie poi a magnetycznego ma tylko jedną składową

Po podstawieniu wzoru (7.24) do zależności (7,27) i (7.28), otrzymujemy

E_Jt = F_l(z-vt)+F₁(z + vt),

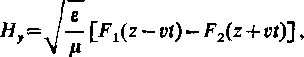
(7.29)

gdzie:

(7.30)

F,(u)-/;(u),    F_a(u)-/J(u).

Z wzorów (7.29) wynikają następujące wnioski: natężenia pola elektrycznego i magnetycznego są superpozycją dwóch fal, a mianowicie fali pierwotnej i fali odbitej zaś wektory E oraz H elektromagnetycznej fali płaskiej są do siebie prostopadłe i znajdują się w płaszczyźnie prostopadłej do kierunku rozchodzenia się fali.

Elektromagnetyczna fala plaska jest falą poprzeczną, bowiem nie zawiera składowych wektorów E oraz H w kierunku rozchodzenia się fali, czyli £"„=//,=0. Falę elektromagnetyczną tego rodzaju oznacza się symbolem TEM, będącym skrótem terminu angielskiego „Transverse Electromagnetic”.

7.4. Twierdzenia Poyntinga

Rozpatrzymy pole elektromagnetyczne w jednorodnym środowisku, wobec czego e=const, p=const, y=const.

Mnożąc skalarnie pierwsze równanie Maxwel!a (7.1) przez E, zaś drugie równanie Maxwella (7.2) przez H, otrzymujemy

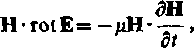
(7.31)

div[E x H]=H-rotE—E-rotH,

znajdujemy

5E    3H

-div[ExH]=E-J + £E- —+ #iH---

dl    dt

Otrzymane równanie całkujemy w obszarze v, wobec czego

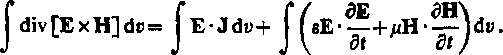
v    c    v

:* po odjęciu 'tronami, mamy

K * rot H - H • rot E -- K * J +cE Przy uwzględnieniu tożsamości wektorowej

dli

'di

+/(H

dii

dl '

(7.32), .

>a mocy twierdzenia Gaussa-Ostrogradskiego mamy

Jdiv[ExH]di>= f [E x H] ■ dS,

»    Stu)

gdzie S(t.') jest powierzchnią ograniczającą obszar v, zaś wektor dS skierowany jest na zew nątrz tej powierzchni. Wyrażenie (7.32) przybiera zatem postać

- (j> [ExH]*dS= |E-Jdu+

S (p)    p

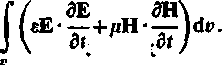
(7.33)

Przypuśćmy, że w części obszaru c wytwarzana jest energia elektryczna kosztem innej postaci energii, na przykład znajdują się w nim źródła energii elektrycznej. Wówczas (por. wzór 1.60)

J=y[E+E₍J,    (7.34)

gdzie: E„ jest natężeniem narzuconego pola elektrycznego, wywołanego działaniem czyn-^ ników obcych w stosunku do pola elektromagnetycznego. W części obszaru, gdzie nic występuje zjawisko wytwarzania energii elektrycznej mamy E„=0.

Z zależności (7.34) otrzymujemy

wobec czego

Mamy

J

E----E„,

y

E-J=Ij²-E„-J,

y

\

(7.35)

ÓE

dt

d „A 1 d    1 5E    1

5tV2 ) 2 dt    2 dt    2

czyli

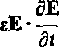
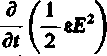
(7-36)