Image29 (20)

56

Rozwiązaniem ogólnym tego równania jest rodzina krzywych

ln (Cr)

cpu

vV - u² ’

z której wybieramy jedną, przechodzącą przez punkt początkowy o współrzęd nych (r₀, a). Dla tej krzywej stała

C =

1

a u

S V² — U²

Zatem szukany tor samolotu będzie dany wzorem

r =

^ro ^e

(a ~ <P)u

'Z

Współrzędne końca toru (r_k, (p_k) dane są równościami

r,. =

(a — ic)u

y/ y* yi

^ro e

1.21

ds

Ct

^a) ^v = Jt ⁼ c s<> e”

b) a, =

dv

dt

= c² s_Q e^ct,

“n = ^at łg^a = c¹ so e^ct tg«,

v²

c) P = — = s₉ ctga.

^an

Gdy a = 0, wtedy a_n — 0, co odpowiada nieskończonemu promieniowi krzywizny, zatem mrówka porusza się po prostej.

1.22

r = c/<p, (p = a + bt. Dla t = 0 r(0) — c/a = r₀

a + bt . bt

a

W przypadku b/a > O punkt porusza się po spirali w kierunku do środka. Jest to ruch ograniczony w przestrzeni i trwający nieskończenie dhigo (r -> 0,

t —► oo).

W przypadku b/a < 0 punkt porusza się po spirali w kierunku na zewnątrz. Jest to ruch nieograniczony, ale czas ruchu jest skończony (r -► oo, gdy

t -> —a/b).

W przypadku b > 0 torem ruchu jest spirala prawoskrętna, w przypadku b < 0 - spirala lewoskrętna.

1.23. Przyjmujemy współrzędne i oznaczenia jak na rys. 15. Układ biegunowy:

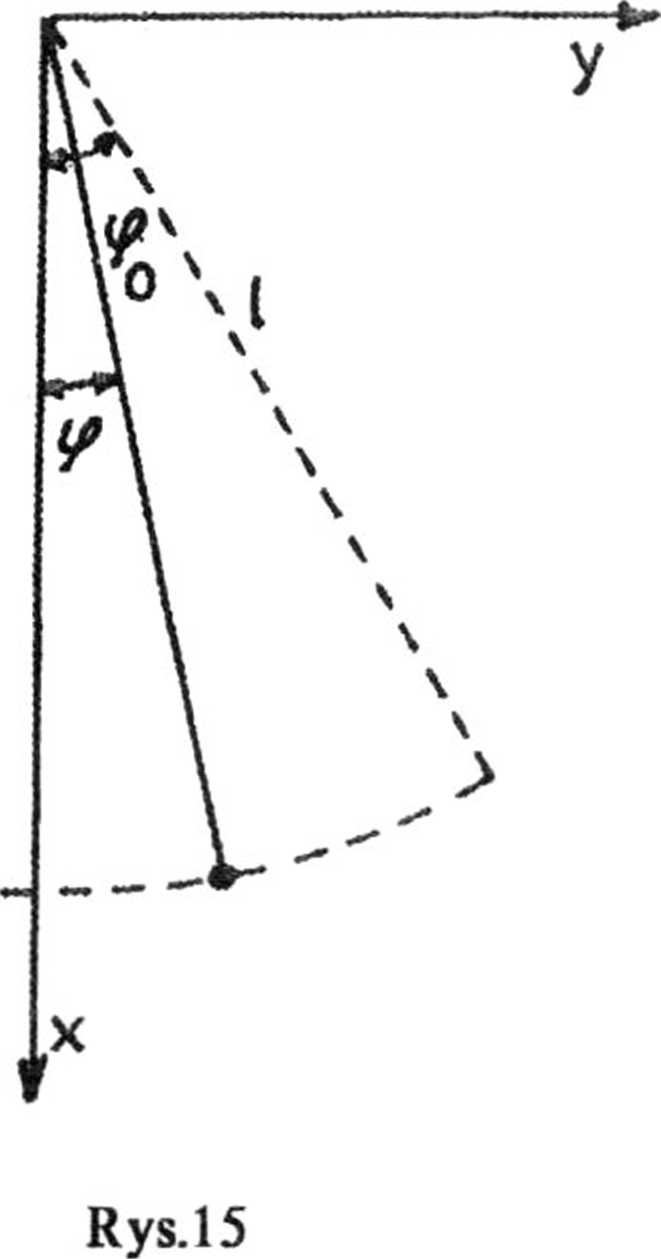
r = l,

(P

Cp COS (Ot,

gdzie ca - częstość drgań wahadła. Prędkość:

v_r = r = 0,

v = rep = —lq> a) sincot,

v

l (p. ca sincot.

Przyspieszenie:

a_r = r — rep² = —l(p²0co² sin²cot, dy = rep + 2rcp — —l(p₀co² coscot,

a = / (p_Q co²y/cos²cnt + cp% sin^cot. Układ kartezjański:

x = r coscp = / cos(ę_Q coscut), y = r sin cp = l s in(cp₀ co scot),