Image0075 BMP

W łych warunkach równania Muxwellu przybierają postać:

(8.25)

(8.26)

rot II = yE, rotE= — jcu^H.

Należy pamiętać o tym, że w niniejszej pracy norma wektorów zespolonych charakteryzujących harmoniczne pole elektromagnetyczne jest zawsze równa wartości skutecznej odpowiedniego wektora,

8.3. Twierdzenie Poyntinga w postaci zespolonej

Rozpatrzymy harmoniczne pole elektromagnetyczne w jednorodnym środowisku, przy czym w rozpatrywanym obszarze pola nie występuje zjawisko wytwarzania energii elektrycznej kosztem innej postaci energii. Niech e, p, y oznaczają przenikalność elektryczną i magnetyczną oraz konduktywność środowiska, będące wielkościami stałymi

Zespolonym wektorem Poyntinga nazywamy iloczyn wektorowy ExH*, gdzie H* oznacza wektor sprzężony (por. wzór 8.8).

s

Obliczymy strumień zespolonego wektora Poyntinga | [E x H*] dS przez powierzch

nię zamkniętą S, która jest brzegiem obszaru v. Na podstawie twierdzenia Gaussa-Ostro-gradskiego mamy

$ [E x H*]- dS = f div [E x H*] dr.

(8.27)

V

Do tożsamości wektorowej

div [E x H*] = H*' ro t E - E • ro t H*

podstawiamy rotE z równania (8.24) oraz równanie

rot H* = (y —jcoe) E*,

wynikające ze wzoru (8.23) dla wielkości zespolonych sprzężonych, otrzymując

div [E x H*] = - ja»n| |H] |² - (y - jwe)||E| |²,

zgodnie z określeniem normy wektora zespolonego. Po podstawieniu tej zależności do wzoru (8.27), mamy

- $ [ĘxH*]'dS=fyj|Ej|ⁱdt₎+j2taf(iAtI|Hl|²-i8[|E|j²)dt₎,

u    u

a przy uwzględnieniu wyrażenia J = yE znajdujemy j[ Jj| = y||E|J, wobec czego otrzymujemy w wyniku

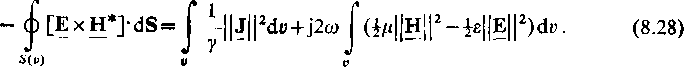
Omówimy kolejno poszczególne wyrazy powyższego równania.

Catka powierzchniowa — J [ExH*]*dS, ze względu na znak minus, przedstawia

strumień zespolonego wektora Poyntinga wnikający od wnętrza obszaru r przez jego

powierzchnię graniczną S. Zgodnie z rozważaniami podanymi w p. 8.1.2, wielkość t(j||* pi /ulstawia wartość średnią za okres gęstości objętościowej mocy przetwarzanej na ciepło, wobec czego całka objętościowa J* ■ ||j|j²de jest równa wartości średniej za okres mocy

l>

przetwarzanej na ciepło w obszarze v, czyli jest równa mocy czynnej związanej z tym obszarem. Wielkość -J-/z||H|]² jest równa średniej wartości za okres gęstości objętościowej energii pola magnetycznego, a całka J^g||H]|²dr przedstawia wartość średnią za okres

V

energii pola magnetycznego zawartej w obszarze r. Podobnie całka J |e|J²dxr jest równa

Iż

sicdniej wartości za okres energii pola elektrycznego zawartej w rozpatrywanym obszarze.

Pomnożona przez 2vt różnica średnich wartości za okres energii pola magnetycznego i pola elektrycznego zawartych w obszarze u jest mocą bierną związaną z tym obszarem. Należy przy ty ni zauważyć, że moc bierna związana z polem magnetycznym jest dodatnia, a moc bierna związana z polem elektrycznym jest ujemna. Wielkości te są odpowiednio równe mocy biernej indukcyjnej i pojemnościowej.

Oznaczając przez P moc czynną, a przez Q moc bierną związaną z obszarem v, fnamy

(8.29)

/

(8.30)

Z powyższego wynika, że prawa strona równania (8.28) przedstawia moc zespoloną V P+jQ związaną z obszarem u, wobec czego

S=- § [ExH*]-dS.    (8.31)

S(i-)

Moc zespolona związana z obszarem v jest zatem równa strumieniowi zespolonego wek-<or;t Poyntinga wnikającemu do wnętrza obszaru przez jego granicę. Zespolony wektor 1’oyniinga nazywany jest gęstością powierzchniową strumienia mocy zespolonej, a całka /awaria w zależności (S.31) — strumieniem mocy zespolonej.

Z powyższych rozważań wynika twierdzenie Poyntinga w postaci zespolonej: strumień mocy zespolonej wnikający do obszaru przez jego granicę równa się mocy zespolonej zwią-.iinej z tym obszarem.    '

Twierdzenie Poyntinga w postaci zespolonej umożliwia przedstawienie mocy zespolonej /wiązanej z pewnym obszarem w postaci strumienia mocy zespolonej wnikającej do wnętrza icg.o obszaru przez jego granicę. Twierdzenie to znajduje zastosowanie przy obliczaniu mocy czynnej przetwarzanej na ciepło w obszarze, a także przy obliczaniu impcdancji wewnętrznej przewodów' (por. np, p, 8,5,2).

K.4, Potencjał wektorowy i skalarny

((mówimy potencjały zespolone opisujące harmoniczne pole elektromagnetyczne w icdnorodnym środowisku o stałych parametrach p, y.

Przypuśćmy. Że w pewnym obszarze r pola istnieje ładunek przestrzenny o gęstości