7292101060

410

Miernictwo.

IV-rzęćLnych wagi jednakowe, równania normalne przybierają postać uproszczona:

......(24*)

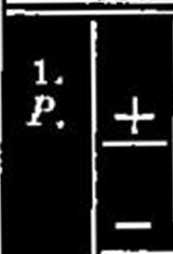
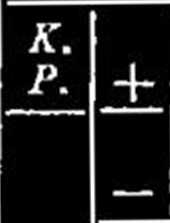
[a a] 0x -j- [a &] Z_y -}- [a Z] = o \ci 6] Qx ~{-* \b b\ [6 ?] *= o ;

oczywiście, że i [/; o o] zmienia się na [o o]...........(25*)

Przykład wcinania wprzód z wyrównaniem. Punkt P wcięto nie tylko z puok-Ww (1) i (2) (patrz przykład str. 403.), lecz także i z punktu A”, nawiązując gie n» kaziłem stanowisku do jednego punktu stałego. Przy pomocy spółrzednych przybliżonych ad i o my potrzebno do rachunku (a)^ł (przybliżono), oraz spółozynniki rówa bł a i b

y,

y_P

Vi

log A y log A x log tg rp

. I

(«)». I)

log sin <p log cos rp compl. log s log <pⁿ

logardogg"^^

^,<r Kontrola

logó=logn"~-log(Ax-\-Ay\ *^L s log^z-dy) fl    log tg ip

(znak A y),    y>

,    ^b .    (")/>. ł + ^°

(zn. przeciwny A z)

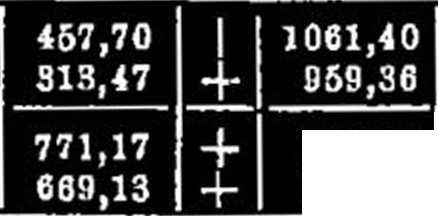
184,48

313,47

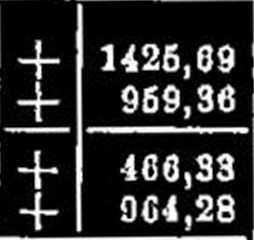
1 =

2,6971857 » 2,6686934

0,0284923)1 <p=46°52'41"

313° 7' 19" 133° 7'19"

a =

b —

2,34375

2,31526

1,4999619 łl 2,9842032

—    220,7

—    200,7

OOp.i +⁴^^0=:

= 3-58° 7' 1

460,70

313,47

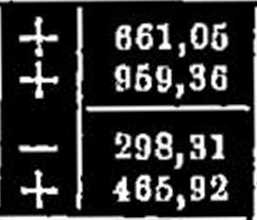
2,88322411» 2,4746678)1

0,4085663

7>=68°40'38"

9,96920

9,56064

7,08598

5,31442

2,36960

1,96104

a *1 — 234,2 91,4

3,0203458 h 2,6683114

o —

248°40'38"

G8“40'S8"

0,3580339 JJ yj = 06° 19' 22"

= 293°40'33"

2.

P. +

2,8871501m

2,0087704

102,04    0,8783797

873,21 «p=S2°27'46"

9,99623

9,11786

7,10908

6,31442

2,41973

1,54135

a —

b —

—    262,9

—    34,8

2,8255106

2,9411187

9,8843910 = 37° 27' 4

277°32'15" 97°32'15"

(a)^.2 + 45*=*

= 322° 32^,,15”

Kierunki wcinające nawiązano na punktach stałych (1) 1 (2) do kierunku (1)—(2). na punkcie K do również stałego kierunku K—L.

Średnie, utworzone ze spostrzeżeń na stanowiskach (1), K i (2), zorientowano wedk azymutów pozornych ₂ (^a)j\ l i («)$ l ^:

Stanowisko: (1)

Stanowisko K

Cel do (2) , n P	0° 0' 0" 276°15'O0"	Cel. do L ! 0° 0' 0" „ „ P 285° 19'18"
(«)l. 2	= 210°62' 13"	(a)k'i= 14S°21'16"
A'o Wp 1 A'0 + 180«X	133°07'19" = 313° 07' 19" = 319°07'19''	A'0= 68°40'34" (°) p.A ^= 248° 40'38" (A’)0 -f 180°)* = 248°40' 34"
	= 0	•s •% + II

Cel. do (1) .    « P

K₀ Wp. 2

(A’₀) 4-130°),

Stanowisko (2)

0° 0^r o"

60° 40'02" (a)_2al= 36° 62' 13"

97°32'15" 277°32'16" 277°32^,16"