Strona0227

227

Równanie różniczkowe mchu drgającego masy m przybiera postać: my + k_zy = 0 lub

y+—— y = 0 mS_n

gdzie:

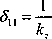
hi - sztywność zastępcza układu,

S_u~ przemieszczenie pionowe masy m przy działaniu jednostkowej siły

(P= IN).

Częstość drgań własnych

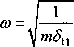
(9.56)

Przemieszczenie belki w miejscu przyłożenia siły ? = 1 N znajdziemy metodą Maxwella-Mohra

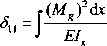
(9.57)

gdzie: M_g - moment gnący od siły jednostkowej.

Belka jest układem jednokrotnie statycznie niewyznaczalnym, W celu wyznaczenia równania momentów gnących znajdziemy reakcję podporową R_A. W tym celu zastosujemy twierdzenie Menabre’a, wg którego

dR_A

gdzie: V— energia potencjalna zginania

Równania momentów gnących przy działaniu siły P przybierają postać M_g(x) = —R_Ax dla 0<;e</

M_g(x) = -R_Ax + P(x-l) dla l<x< 21