Matematyka 2 !7

216 IV. Równania różniczkowe znycrajne

a prawa strona

P = 2y(x)-2x^: + 1 = 2x + 2x^: -2e^:' -2x^: -r 1 = 1 + 2x -2e"\ więc dla funkcji y = y(x) określonej wzorem (I) równanie (2) jest spełnione dla każdego x eR. Funkcja (I) jest rozwiązaniem równania różniczkowego (2).    ®

PRZYKI AD 1.2. Weźmy pod uwagę równanie

O)    y'=2x.

Równanie rozważamy w dziedzinie naturalnej funkcji f(x.y) = 2x. tzn. dla (\,y) eD- R\ Każda funkcja postaci

(2)    y = x^: + C. x el = (-oo,-ł-ao)_t CeR.

jest rozwiązaniem równania (1), przy czym innych rozwiązań określonych na przedziale I równanie nie ma.

Rozwiązania te stanowią jednoparametrową rodzinę funkcji, a ich wykresy (krzywe całkowe równania (1)) są jednoparametrową rodziną parabol, z których kilka przedstawiono na rysunku 1.1.

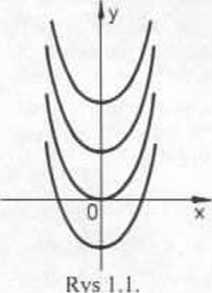
Mówimy, że wzór (2) określa rozwiązanie ogólne (całkę ogólną) równania (1).

Zauważmy, że przez każdy punkt płaszczyzny przechodzi dokładnie jedna krzywa całkowa rozważanego równania. Wyznaczymy na przykład tę krzywą całkową, która przechodzi przez punkt P₀(l,2). Oznacza to. że należy tak dobrać C we wzorze (2). by dla x = I otrzymać y = 2. Podstawiając \ = I i y = 2 we wzorze (2) otrzymujemy C = l.

Krzywa całkowa spełniająca podany warunek jesł więc określona wzorem

y = x^: +1, x €I = (—30,+ao).

Inaczej mówiąc, znaleźliśmy to rozwiązanie równania (I) na przedziale I, które spełnia tzw. warunek początkowy y( 1) = 2.

Dodajmy, że rozwiązaniem równania (1) jest także każda funkcja określona wzorem

y = x^: +C, xe(a,P). CeR,

gdzie (a,|ł) jest dowolnym przedziałem zawartym w przedziale

I =(—OO_t + QO).    ■

Załóżmy, że funkcje

(a) y = y,(x). xel, oraz (b) y = y₂(x),xel₂ są rozwiązaniami równania różniczkowego (1.2), przy czym 1, c: 1₂ oraz y,(x) = y_;(x) dla każdego x el,.

Rozwiązanie (a) nazywamy zawężeniem rozwiązania (b) do przedziału 1,, a rozwiązanie (h) nazywamy przedłużeniem rozwiązania (a) na przedział !,, przy czym (b) nazywamy przedłużeniem właściwym rozwiązania (a), gdy l,cl₂ i i, *1₂.

Rozwiązanie

(c)    y = y(x), x el,

równania różniczkowego nazywamy rozwiązaniem globalnym, gdy nie istnieje rozwiązanie tego równania, które jest przedłużeniem właściwym rozwiązania (c).

Na przykład funkcja

y=x² - I, x el = (-», t-oo),

jest rozwiązaniem globalnym równania (I) rozpatrywanego w^r przykładzie 1.2. Łatwo widać, że każde zawężenie tego rozwiązania, czyli funkcja

y = x²-l, x e(o,(5),

gdzie (a,|J) jest przedziałem zawartym w przedziale 1 = (-ac,4-ao) jest także rozwiązaniem tego równania. Wzór (2) w przykładzie 1.2 określa wszystkie rozwiązania globalne równania (1)