Matematyka 2 )3

292 IV. Równania różniczkowe zwyezajnt

i jest nazywane równaniem liniowym II rzędu o stałych współczynnikach.

Ponieważ umiemy już dla dowolnych a,,a_: eR znaleźć rozwiązanie ogólne równania jednorodnego y" + a,y' + a_:y = 0. więc Stosując poznaną już metodę uzmienniania stałych możemy znaleźć rozw iązanic ogólne równania liniowego niejednorodnego (6.13).

PRZYKŁAD 6.8 Rozwiążemy równanie

(I)

(i)    y”+y * = —^L-

I + C

(2)

y" + y’ = 0.

Najpierw rozwiążemy rów^rnanie jednorodne

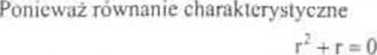
ma dwa pierwiastki: r = 0, r = —I, więc rozwiązanie ogólne równania jednorodnego (2) określone jest wzorem:

y₀=Cr+C₂c \ x€R. C,.C_:eR.

Szukamy rozwiązania szczególnego równania (I) w postaci

y»=C_l(x) + C₂(x)c~\

Niewiadome funkcje Cj(x) i C₂(x) wyznaczymy z układu równań (por.

(6.9))

Kolejno otrzy mujemy

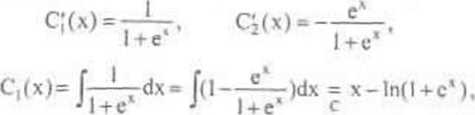
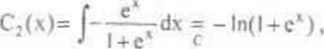
a następnie

y, = x-ln(l + e*)-e“ln(l + c*)_ł

czyli

y, * x-(l + e'^x)ln(l + e*).

Zgodnie z tw ierdzeniem 6.5

y « y₍, + y, = c, + C₂c ' -ł-x-(l+e'*)ln(l+c'), x cR.

gdzie C,, C₂ sit dowolnymi stałymi, jest rozwiązaniem ogólnym równania (1).    B

METODA PRZEWIDYWANIA dla równań liniowych niejednorodnych o stałych współczynnikach Weźmy pod uwagę równanie (6 13): y" + a,y* + a,y = q(x). W pewnych przypadkach, podobnie jak dla równania liniowego I rzędu, potrafimy przew i d z i e c postać rozw iązania szczególnego tego równania i wyznaczyć takie rozwiązanie z pominięciem całkowania (które zawsze występuje przy stosowaniu metody uzmienmania stałych}.

I. Jeżeli w równaniu (6.13>

q(x) = W_n(x)c“.

gdzie a e R, a VV_B jest wielomianem stopnia n. to istnieje rozwiązanie szczególne równania (6.13)postaci

y» = x^kP„(x)e^a\

gdzie P„ jest pewnym wielomianem stopnia n. zaś k - krotnością pierwiastka a równania charakterysty cznego (gdy u nie jest pierwiastkiem równania charakterystycznego, przyjmujemy k = 0/

Na przykład:

a)    dla równania y* -y = x^: + l istnieje rozwiązanie szczególne postaci y, = Ax^: + Bx + C

b)    dla równania y”-y = xc^2ł przewidujemy, że y, = (Ax ^x B)e'¹;

c)    dla równania y’'-y = (x + l)e~* przewidujemy rozwiązanie szczególne w postaci y, = \(Ax + B)e \ gdyż ci = -l jest pierwiastkiem jednokrotnymi równania charakterystycznego r^: -1 = 0;