Matematyka 2 #1

230 IV. Równania różniczkowe zwy czajne

Uwaga. Równanie o zmiennych rozdzielonych może posiadać ponadto pewne rozwiązania szczególne przebiegające poza obszarami, w których spełnione są założenia twierdzenia 2.1. A mianowicie: jeżeli y jest taką liczbą, dla której g(y) = 0. to funkcja stała y = y, x e(a.b). jest rozwiązaniem równania (2.1). Rozwiązanie to może być regularne lub nie (por. przykłady 2.1 i 2.5).

PRZYKŁAD 2.1. Rozwiążemy równanie

o)

Jest to równanie o zmiennych rozdzielonych. Przyjmijmy, że f(x) = 2, g(y) = y- 1. Funkcja fjest ciągła dla x eR. funkcja g jest ciągła i różna od zera dla y ¹ 1 Z twierdzenia 2.1 wynika, że pTzez każdy punkt obszarów

D, = {(x,y) €R“: -oo<x<+oo a -cc<y<l|

oraz

Dj ⁼ {(x,y) cR": -oo<x<-»-oo a 1 <y <-t-oo} przechodzi dokładnie jedna krzywa całkowa równania (I).

Równanie (2.3) określające wszystkie rozwiązania w obszarach D, i D, uzyskujemy przez "rozdzielenie zmiennych" w' równaniu (1) i całkowanie

Zauważmy ponadto, że g(y) = 0 dla y = I Funkcja y - I, x € R. jest także rozwiązaniem równania (1). Dodajmy, że jest to rozwiązanie regularne, co wynika z twierdzenia 1.2 (Cauchy'ego), gdyż prawa strona równania (1) i jej pochodna względem y są funkcjami ciągłymi na całej płaszczyźnie R*.

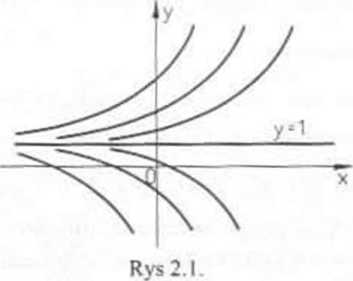
Reasumując, przez każdy punkt płaszczyzny przechodzi dokładnie jedno rozwiązanie równania (I), przy czym wszystkie te rozwiązania

y= l-Ce²*, C>0; y= l + Ce²’. C>0; y = l można zapisać jednym wzorem

y=l+Će²\ x € R, ĆeR.

Jest to rozwiązanie ogolne równania (1). Kilka krzywych całkowych tego równania przedstawia rys. 2.1.    •

PRZYKŁAD 2.2. Znajdziemy rozwiązanie ogólne równania

(1)

dy x

-p -—• dx y

Równanie rozważamy w obszarach D, i D_::

D, = |(x,y) eR‘: -oo<x<+oo a -»<y<0},

= {(x.y) eR²: -ao<x<+oo a l)<y<+ao}.

Wiadomo, zgodnie z twierdzeniem 2.1, że przez każdy punkt tych obszarów przechodzi dokładnie jedno rozwiązanie. Rozwiązania te znajdujemy przez rozdzielenie zmiennych i całkowanie (przed całkowaniem W7god-me jest pomnożyć obie strony przez 2):

1

lniy-l|=2x + C,

gdzie C jest dowolną stałą. Przyjmując C=lnC, C>0, otrzymujemy dalej

In|y — 1|= Ine²' +lnC.

|y-l|=Cc²\ C>0.

Stąd wynika, żc rozwiązania w obszarze D, określone są wzorem y=l-Ce²\ x €(-so.+oo), C> 0, a rozwiązania w obszarze D_: mają postać

y = I ♦-Ce^2t, x e(-¹,+ao), C>0.