Matematyka 2 '1

270 IV Równaniu różniczkowy zwyczajne

Czasem rozwiązanie ogólne otrzymujemy w postaci uwikłanej, to znaczy jest ono określone równaniem

<I>(x, y,C,,C₂) = 0.

I* R Z Y K L A D 5.1. Rozw iążemy równanie

(1)    y" = 6x

przy warunkach początkowych y(0) = 0, y'(0) = - I.

Rozwiązanie ogólne równania (I) znajdujemy przez dwukrotne całkowanie:

y' = 3x^J+C,,

(2)    y = x'+C,x+C,, xeR.

Wzór (2), w którym C, i C_: oznaczają dowolne stałe, okroiła rozwiązanie ogólne równania (I). Uwzględniając warunki początkowo mamy

y(G) = C_:=0.    y'(0) = C,= —I.

Zatem szukanym rozwiązaniem szczególnym jest funkcja

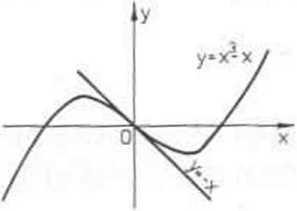
y = x³ - x, x g R

Rys 5.1.    Rys 5.2.

Geometrycznie to oznacza, że krzywa całkowa odpowiadająca temu rozwiązaniu (rys. 5.1) przechodzi przez punkt (0,0) i ma w tym punkcie styczną o współczynniku kierunkowym m = -1.

Zauważmy na koniec, że warunek y(0) = 0 spełnia nieskończenie wiele rozwiązań dunego równania. Są to rozwiązania, dla których y(0) = C₂ =0. czyli funkcje postaci:

y»X³ +C,x. xeR. C, eR .

Oznacza to. Ze przez punkt (0,0) przechodzi nieskończenie wiele krzywych całkowych równania (I). alt* tylko jedna spośród nich (ta. która wcześniej wyznaczyliśmy) ma w tym punkcie styczna o podanym kierunku.    ■

PRZYKŁAD 5.2 Wyznaczymy rozwiązanie równania (1)    y" = I2x² -6x

spełniające warunki brzegowe y( 1) = 0, y(-1) = 2.

Rozwiązanie ogólne tego rów nania określa wzór y = x^J-x³+C,x + C₂. x g R,

gdzie C, i C\ oznaczają dowolne stale. Uwzględniając warunki brzegowe otrzymujemy

y(l) = C, +C₂ -0, y(-l) = 2-C| + C₂ -2.

Stąd C, =0 i Cj = 0. Zatem

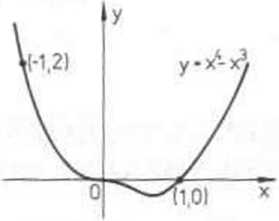
y= x⁴-x³, xeR.

jest rozwiązaniem szczególnym spełniającym podane warunki brzegowe Krzywa całkowa odpowiadająca temu rozwiązaniu (rys 5.2) przechodzi przc2 punkty (1.0) i (-1,2).    ■

Niżej omówimy rozwiązywanie pewnych równań 11 rzędu, które przez odpowiednie podstawienie można sprowadzić do równań 1 rzędu.

RÓWNANIE POSTACI F(x,y\y") = 0. w równaniu (5.2)    F(x,y\y") *= 0

nie występuje w sposób wyraźny niewiadoma funkcja y. Stosujemy podstawienie

y‘ = u(x).

Wówczas y" = u\ Uwzględniając to w równaniu (5.2) otrzymujemy równanie I rzędu:

F(x,u,u') = 0,

^w którym u = u(x) jest funkcją niewiadomą.