Matematyka 2 (5

284 IV Równania różniczkowe zwyczajne

284 IV Równania różniczkowe zwyczajne

y’=*C_l(x)y;(x)+C₂(x)yi(x)

Wówczas (6.8*) oraz

(6.8”) y" = C;(x)y;(x)fC;(x)y;(x) + C₁(x)y;U)^C₂(x)yV(x).

Podstawiając (6.8), (6.8') i (6.8") do równania (6.1) i uwzględniając fa że y, i y₂ są rozwiązaniami równania (6.2), otrzymujemy

c;(x)y;(x)+c;(x)y;<x) = q(x).

(6.9)

Stąd wynika, ż.c pochodne funkcji C,(x) i C₂(x) spełniają układ równan C;(x)y,(x)+C₂(x)y₂(x) = 0, C;(x)y;(x)-i-C₂(x)y;(x)=q(x).

który jest układem liniowym względem niewiadomych Cj(x) i C₂(x). Z liniowej niezależności rozwiązań y, i v_: wynika, ze wyznaczni główny tego układu

W(x)=

y.(*) y2ixj| o

yj(x) y'₃(x)|

dla każdego x 6(a,b). Zgodnie z twierdzeniem Cramera układ (6.9) ma dokładnie jedno rozwiązanie:

c:(x) =

1

W(x)

o y₂(x) q(x) y₂(x)

^C;(x)=ww

y,(x) o

yKx) q(x)

Stąd

W(x)

(6.10) C,(x)= | -$^^UJdx + C,.    C_:(x)= JHi^l!^_{x +} c₂,

gdzie C, i C_: są dowolnymi stałymi

Wykazuje się, że wzór (6.8) z funkcjami C,(x) i C₂(x) określonymi wzorami (6.10) określa rozw iązanie ogólne równania (6.1).

PRZYKŁAD 6 3. Weźmy pod uwagę równanie

(I)    y»₊iy₊-2.y,₌ «l dla x>0.

x x^ł ' x^

Można sprawdzić, że funkcje y = —, x>0 i y = -rr, x>0, są rozwiązaniami szczególnymi równania jednorodnego

(2)

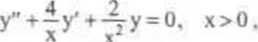
x

pr/> czym są to rozwiązania liniowo niezależne (gdyż ich iloraz nie jest stały). Zgodnie z twierdzeniem 6.3 w-zór

y« - C, +C₂-y, x > 0, C,.Cj€R •' x

określa rozwiązanie ogólne równania (2).

Rozwiązanie ogólne równania (1) znajdziemy w postaci y=c,(x)i+c₂(x)^_t

przy czym pochodne niewiadomych funkcji C,(x) i C₂(x) wyznaczymy z układu równań (por. (6.9)):

c;(x)^-+q(x)-y = o,

•'    X

I    2 c^x

-c;(x)-V-c;(x)4=^.

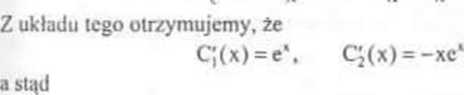
X    X    X*

C,(x) = c^l +C,_f C₂(x) = e‘ -xe' + C₃, gdzie C, i C₃ oznaczają dowolne stałe. Zatem rozwiązanie ogólne równania (I) określone jest wzorem

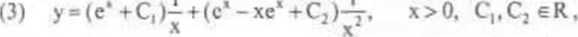
Z twierdzenia 6.1 wynika, że przez każdy punkt obszaru D = |(x,y)eR^: x>0) przechodzi dokładnie jedno rozwiązanie o zadanej wartości pochodnej. Wyznaczymy, na przykład, to rozwiązanie równania (1). dla którego y(I) = e — I oraz y'( 1 )= 2 — e Z wzoru (3) mamy

(4)    y'“—y(xc* -2e^ł -C,x-2C₂).

x

Podstawiając x = 1. y = e -1. y' = 2- e we wzorach (3) i (4) otrzymujemy C, +C₂ =-l,    -C, -2C₂ = 2,

a stąd C, =0. C_: = -l. Zatem rozwiązaniem szczególnym równania (l) spełniającym podane warunki początkowe jest funkcja