Matematyka 2 (9

288 IV. Równania różniczkowe zwyczajne

jedynie do pewnych operacji algebraicznych. Zauważmy także, że każde rozwiązanie równania (6.11) jest określone na całym zbiorze R, czyli dla x e(-ao,+ao).

Wiadomo z wcześniejszych rozważań, że znając dwa liniowo niezależne rozwiązania szczególne tego równania możemy natychmiast napisać jego rozwiązanie ogólne

Z uwagi na postać równania (6.11), rozwiązań szczególnych tego równania szukamy wśród funkcji wykładniczych postaci

y = e”. xeR.

Po obliczeniu y\y'' i wstawieniu do (6.11) okazuje się, że funkcja y = c^,ł jest rozwiązaniem tego równania wtedy i tylko wtedy, gdy współczynnik r spełnia trw. równanie charakterystyczne:

(612)

r² +a,r + a₇ =0.

Rozważymy kolejno trzy przypadki A = af-4a_:>0, A = 0, A<0.

A Jeżeli A > 0. równanie charakterystyczne (6.12) ma dwa różne pierw iastki rzeczywiste r, i r_: Zatem funkcje

y,(x)«e^r'\    y₂(x) = e^r;*

są rozwiązaniami szczególnymi równania (6.11), przy czym są to rozwiązania liniowo niezależne, gdyż

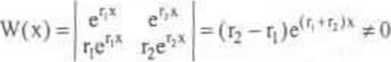
dla każdego x € R. Zgodnie z twierdzeniem 6.3

yaC,c^r,x +C₂e^r,\ xeR, C,,C₂gR, jest rozwiązaniem ogólnym równania (6 11)

PRZYKŁAD 6.5. Znajdziemy rozwiązanie ogólne równania

(1)

y" +2/-3y = 0.

Ponieważ równanie charakterystyczne r² +2r-3 = 0

ma dwa pierwiastki: r, = 1 i r₂ =-3, więc

y=C,e* + C_:c^-1\ x€R, C,.C₂eR, jest rozwiązaniem ogólnym równania (1).    ■

B Jeżeli A = 0. to równanie charakterystyczne (6.12) ma jeden (podwójny) pierwiastek: ^ = -^-a,. Funkcja y,(x) = e^rv jest rozwiązaniem szczególnym równania (6.11). Wykażemy, że w tym przypadku funkcja y,(x) = xe^r* jest również rozwiązaniem tego równania. Obliczamy

y₂(x) = (I + r₀x )c^v, y₂'( x) = r₀( 2 + r₀x )e^r *, wstawiamy do równania (6.11) i otrzymujemy:

c^r°‘((r* r_na, + a₂ )x + 2r_o + a,) = 0.

Ponieważ r„ + r„a, + a₂ = 0 (r₀ jest pierwiastkiem równania (6.12)) i r_(ł =    więc równanie jest spełnione dla każdego x eR. Oznacza to.

że funkcja y₂(x) = xe^r'* jest rozwiązaniem równania (6.11).

Rozwiązania y,(x) i y₂(x) są liniowo niezależne, gdyż

W(x) =

c^v

xc^r‘*

tbe^f"* (l + rox)e^r^

* 0

dla każdego x eR.

Zgodnie z twierdzeniem 6.3

y = C,c^,,x + C₂xe^v\    xeR. C,,C₂eR,

jest rozwiązaniem ogólnym równania (6.11).

PRZYKŁAD 6.6. Znajdziemy rozwiązanie ogólne równania

(I)    y"i-2y' + y = 0.

Ponieważ rów-nanie charakterystyczne r +2r + l = 0

ma pierwiastek podwójny r₀ = - I. więc rozwiązanie ogólne równania (I) określa wzór

y = C,e~* + C₂xe"\    xeK, C,,C₂ eR