Matematyka 2 &5

264 IV Równaniu różniczkowy zwyczajne

Następnie znajdziemy rozwiązanie szczególne równania (1) spełniające warunek y(-l) = l. Podstawiając x = -l i y= I w (2) otrzymujemy C = 4. Zatem szukanym rozwiązaniem jest funkcja uwikłana y « y( x) określona równaniem

x²y-x' + y³ + y-4 = 0.

dla której y(-l) = l. Taka funkcja, zgodnie z twierdzeniem o istnieniu funkcji uwikłanej, jest tylko jedna.    ■

CZYNNIK CAŁKUJĄCY. Jeżeli dla funkcji P i Q w równaniu (4.1) nie jest spełniony warunek (4.2), to równanie to nie jest równaniem zupełnym. W pewnych przypadkach można wyznaczyć taką funkcję p = p( x,y) klasy C^:. różną od zera na obszarze D. ze

(4.5)    p(x.y)P(x,y)dx + p(x.y)Q(x.y)dy = 0

jest równaniem zupełnym. Funkcję p nazywamy wtedy czynnikiem całkującym równania (4.1).

Czynnik całkujący p spełnia więc równanie: czyli

(4.6)

Jeżeli p jest funkcją tylko jednej zmiennej: x albo y. to rozwiązanie tego równania me jest trudne. W dalszym ciągu ograniczymy się do tych dwóch przy padków.

1. Przypuśćmy, że istnieje czynnik całkujący zależny tylko od zmiennej x, czyli p = p(x) Równanie (4.6) możemy zapisać w postaci

pP; = p'(x)Q + pQ;, skąd (Q * 0 na obszarze D) otrzymujemy

(4.7)

Jeżeli prawa strona lego równania nie zależy od zmiennej y. to przy o-znaezeniu

A(x)

p;-q:

Q z rów nania (4.7) W7nika, że

M(x)=e^,A'^,,,h.

| odwrotnie: łatwo sprawdzić, że funkcja p określona tym wzorem jest czynnikiem całkującym równania (4.1).

II. Analogicznie, gdy funkcja P jest różna od zera na obszarze U oraz wyrażenie (Q* - P,' )/P me zależy od zmiennej x. to istnieje czynnik

całkujący p zależny tylko od zmiennej y. przy czym

^y)_=elB|»|dV_i

gdzie

q; - p;

B(y)=-V^

PRZYKŁAD 4.2. Równanie

(I)    y²(x-y)dx + (l-xy^:)dy=0

nie jest równaniem zupełnym. Zapiszmy to równanie w postaci normalnej:

dy _ y^;(y-x) dx I — xy²

y³( \_ _ , |

Prawa strona tego równaniu f(x,y) = -—-—r¹ i jej pochodna f' są

l-xy

funkcjami ciągłymi na każdym obszarze, w którym I - xy² * 0 (rys 4.1).

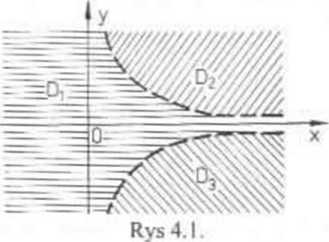
Z twierdzenia 1.2 (Cauchy‘ego) wynika, że przez każdy punkt tych obszarów przechodzi dokładnie jedno rozwiązanie równania (I). Inaczej mó-wiąc, w obszarach D,,D₂ i D₃ (rys. 4.1) ma miejsce jednoznaczność rozwiązań równania (I).