Matematyka 2 #5

234 IV, Kównama różniczkowe zwyczajne

_v/y = x-*-C. CeR, x + C>0.

Stąd otrzymujemy rozwiązanie ogólne równania (1): (2)    y = (x + C)², CeR, x + C>0.

Przyjmując w (2) x = 4 i y = 1 otrzymujemy

1 = (4 + C)², 4 + C> 0,

skąd wynika, że C = -3. Rozwiązanie szczególne spełniające warunek y(4)= 1 określone jest więc wzorem

y = (x-3)². x>3.

Czytelnikowi pozostawiamy naszkicowanie kilku krzywych całkowych równania (1), w tym krzywej całkowej przechodzącej przez punkt (4,1).

■

PRZYKŁAD 2.5. Rozwiążemy równanie

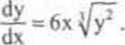
(I)

Przez każdy punkt obszarów

D, = |(x,y) €R⁷: -oc<x<+oo a 0<y<+ao},

D₂ ⁼ U^x*y) eR*: -oo<x< +co a -oc<y<0} przechodzi dokładnie jedna krzywa całkowa tego rówmania (tw.2.1). Rozdzielając zmienne w równaniu (I) i całkując otrzymujemy:

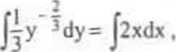
(2)

y' =x^: + C, y = (x² + C)\

gdzie C jest dowolną stałą Wzór ten określa rozwiązanie ogólne rówma-nia (1). Ponadto funkcja y = 0, xeR, jest rozwiązaniem szczególnym tego równania, przy czym nietrudno sprawdzić, źe jest to rozw iązanie osobliwe. Rysunek 2.3 przedstawia krzywe całkowe tego równania

Z dokładniejszej analizy rozwiązania ogólnego (2) wynika, że: a) rozwiązania, których wykresy przebiegają w obszarze D, są określone wzorami

y = (x^:+C)\ C>0, x e(-co,+oo), y = x\ x e(-co.O); y = x\ xe(0,+oo), y = (x^:+C)^J. C<0. x €(-oo,—y^Ć), y = (x²+C)\ C<0, x e(V^C,+oo);

h) rozwiązania, których wykresy przebiegają w obszarze D_: są określone wzorami

y = (x^,+C)^J, C<0.    ■

Uwaga. Na ogół pomijać będziemy szczegółową analizę rozwiązań równania. Celem naszym będzie uzyskanie wspólnego wzoru określającego wszystkie lub prawie wszystkie rozwiązania, czyli znalezienie rozwiązania ogólnego danego równania różniczkowego.

PRZYKŁAD 2.6. Rozwiążemy równanie (1)    ^ = 2x(y^J-y).

Zakładamy, że xeR₍y*0iy*l. rozdzielamy zmienne i cał

kujemy:

dy

y^:-y

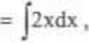
J(^“^)dy=J^2xdx-

lnj——-I®x² +InĆ. C>0, y

l~~l= Cc*^ł, C>0,

Ponadto funkcje y = 0iy=IdlaxeR są rozwiązaniami szczególnymi równania (1). Zatem w^ory

pyi|=Ce^,J, C>0; y=0; y=l

określają wszystkie rozw iązania tego równania. Można je zapisać w postaci: