Matematyka 2 $7

246 IV /W* nam a różniczkowe zwyczajne

Zgodnie z założeniem, prawa strona tego równania f(x,y) = -p(x)y + q(x) oraz jej pochodna f_y'(x,y) = -p(x) są funkcjami

ciągłymi na obszarze D. Z twierdzenia 1.2 (Cauchy’cgo) o istnieniu i jednoznaczości rozw iązań równania y'= f(x,y) wynika natychmiast, że przez każdy punkt obszaru D przechodzi dokładnie jedna krzywa całkowa równania (3.1).

W dalszym ciągu przyjmujemy, źe funkcje p i q są ciągłe na przedziale (a,b), przy czym przedział ten może być niewłaściwy.

Rozwiązanie równania liniowego jednorodnego. Zauważmy, że równanie liniowe jednorodne (3.2) jest równaniem o zmiennych rozdzielonych:

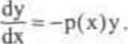
Jednym z rozwiązań lego równania jest funkcja y = 0, x e(a,b). Zakładając, że y * 0. rozdzielamy zmienne i całkujemy

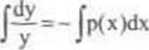
Oznaczając przez P dowolną z funkcji pierwotnych funkcji p na przedziale (a,b) (tzn., źe P'(x) = p( x)) mamy:

ln|y|=-P(x)+ InĆ, Ć>0 |yj=Ce'^p,°, C>0.

Dołączając do tego rozwiązanie szczególne y = 0 otrzymujemy wzór

(3.3)

y = Ce-^p,,\ CsR, x_€(a,b).

który określa rozwiązanie ogólne równania (3.2), przy czym zawiera on wszystkie rozwiązania tego równania.

METODA UZMIENNIANIA STAŁEJ rozwiązywania równań liniowych niejednorodnych Wykażemy, źe każde rozwiązanie równania (3.1) można otrzymać ze wzoru (3.3) zastępując stałą C odpowiednio dobraną funkcją C(x).

Przypuśćmy najpierw, źe C(x) jest już tak dobraną funkcją, że

y = C(x)c^p,ł\ x e(a.b),

jest rozwiązaniem równania (3.1). Zatem

C'(x)c"^p<*⁾ -C(x)e"^ru,P'(x) + p(x)C(x)e"^p,° = q(x).

a stąd

_C(x)_e-"»' = _q(x),

C(x)= Jq(x)e^p,”dx,

czyli

C(x) = Q(x) + C,

gdzie C oznacza dowolną stałą, a Q - dowolną z funkcji pierwotnych funkcji q(x)e^Płłł. W konsekwencji

(3.4)    y = (Q(x) + C)e^p<0,

gdzie C jest dowolną stałą, P'(x) = p(x), Q'(x) = q(x)e^,,<’° dla x e(a,b).

1 odwrotnie: łatwo sprawdzić (przez podstawienie), że każda funkcja postaci (3.4) jest rozwiązaniem równania (3.1) na przedziale (a.b).

Co więcej, wzór (3.4) zawiera wszystkie rozwiązania równania

(3.1) , gdyż dla dowolnego punktu (x₀,y₀) eD można dobrać taką war

tość stałej C w (3.4), źe rozwiązanie określone tym wzorem spełnia warunek y(x₀) = y₀. Istotnie: podstawiając w (3.4) x = x₀iy = y₀ otrzymujemy y₀ =( Q( x₀)+ C )e    , skąd C = y₀e^,u#,-Q(x₀).

Oznacza to, że wzór (3.4) określa rozwiązanie ogólne równania

(3.1) , przy czym zawiera on wszystkie rozwiązania tego równania w obszarze D. Dodajmy, że wszystkie te rozwiązania są określone na całym przedziale (a.b).

Metodę uzyskania wzoru (3.4) ze wzoru (3.3) nazywamy metodą uzmienniania stałej.

Zauważmy jeszcze, że rozwiązanie (3.4) można zapisać w postaci sumy y=y₀(x,C) + y_ł(x). gdzie

y₀ * Ce^_p<t)

jest rozwiązaniem ogólnym równania (3.2), a

y, = Q(x)e-^f<‘>