Strona0198

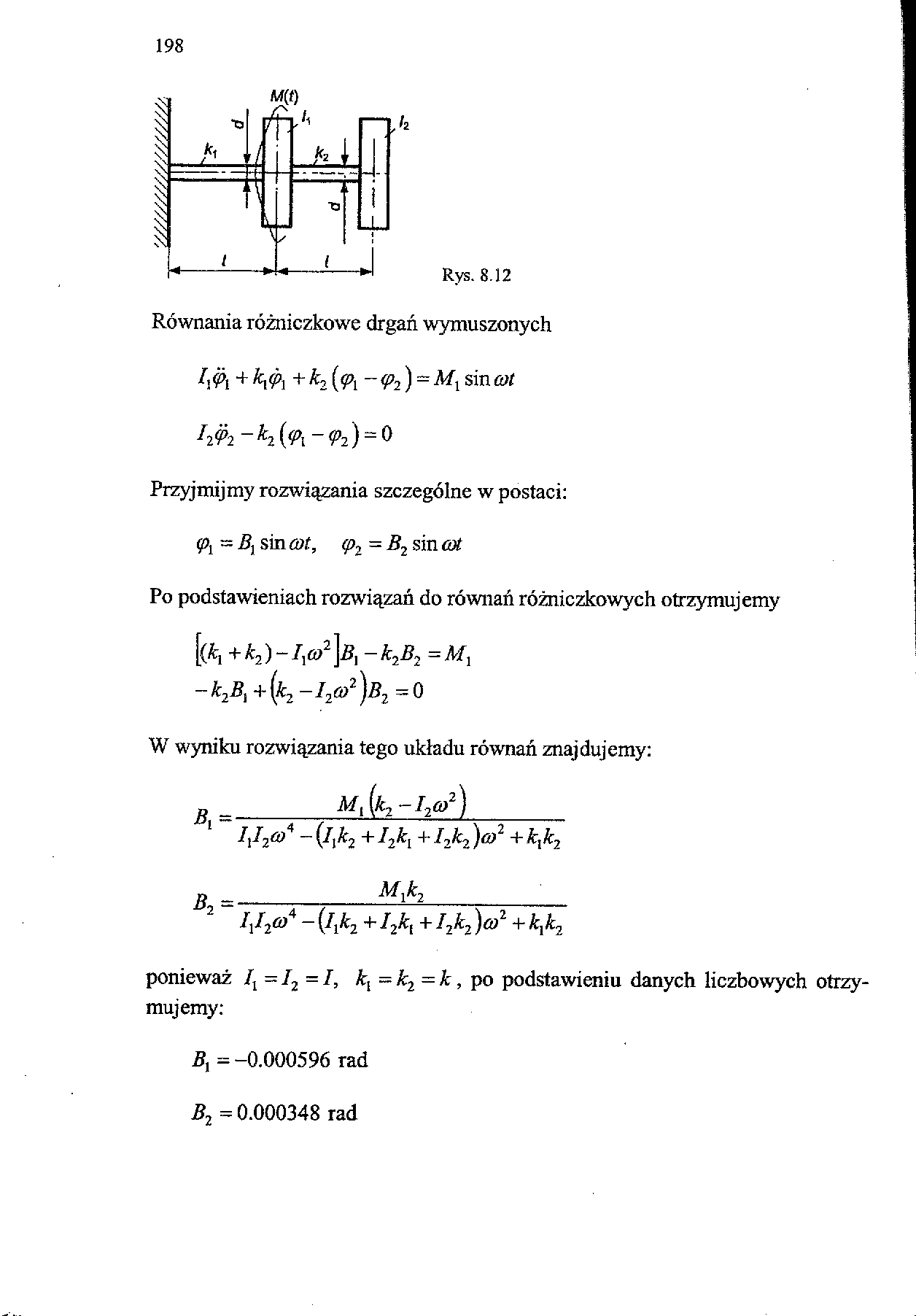
198

Równania różniczkowe drgań wymuszonych l_xę_x + ky(p_x +k₂ [<p_x -<p₂) = M_l sincot h92-K{<Px-<Pi)^ 0

Przyjmijmy rozwiązania szczególne w postaci: ę_x ~ By sin cot, ę₂ = B₂ sin cot

Po podstawieniach rozwiązań do równań różniczkowych otrzymujemy

[(k_x +£₂)-/_]&r]Ą-k₂B₂ =My - k₂By + (k₂ -I₂a>^{1 2 3 4} )b₂ - 0

W wyniku rozwiązania tego układu równań znajdujemy:

1

_B =_M.jth-hm¹)

2

   I_XI₂ĆQ^Ą ~ (lyk₂ + I₂ky + I₂k₂ )o>³ + k_Xk_Z

_B    _MŁ___

3

   /j/₂6J⁵ - (lyk₂ + I₂k_{ + I₂k₂ )(0³ + k_xk₂

4

ponieważ I_x-I₂= I, k_x = k₂ = k, po podstawieniu danych liczbowych otrzymujemy:

5

B_x =-0.000596 rad B₂ =0.000348 rad