skrypt wzory i prawa z objasnieniami51

100 Drgania tłumione

■ Równanie różniczkowe drgań tłumionych otrzymujemy z. drugiej zasady dynamiki zakładając, że oprócz, siły harmonicznej F_h - -k x działa siła oporu ośrodka F_a - -rv. gdzie r jest współczynnikiem oporu ośrodka a v= ^ prędkością

d~x    i dt

m—r = -kx - r~ dr²    d/

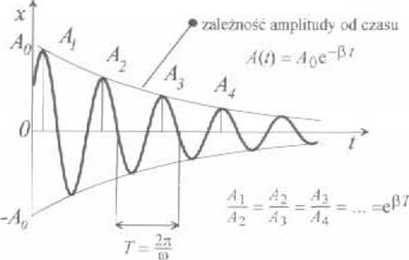
Przenosząc wszystkie składniki równania na łewą stronę i dzieląc przez m otrzymujemy równanie różniczkowe drgań tłumionych w postaci przedstawionej w punkcie 47 ■ Równanie drgań tłumionych w postaci x - A(t) cos (w/ + p| jest słuszne jedynie wtedy, gdy o>, > p. tj. gdy tłumienie nie jest zbył silne. Jeżeli oi₀ <; p mamy do czynienia z ruchem apenodycznym. w którym ciało wychylone wraca do położenia równowagi nie wykonując drgań ■ Wielkość ?. - In ^ fiT nazywa się logarytmicznym dekrementem tłumienia Doświadczalne wyznaczenie wartości I polega na pomiarze kolejnych amplitud układu drgającego (patrz rysunek) i wyznaczeniu

li _ ^Ai _ ^Ąy

An Ay

logarytmu naturalnego ze stosunków

■ Wielkością charakteryzującą układ wykonujący drgania tłumione jest również tzw dobroć układu drgającego Q. Określamy ją następująco

= 7L\'_e .

gdzie Ne jest ilością drgań wykonywanych przez układ, zanim amplituda zmaleje e razy Jak widać z powyższej sekwencji równań dobroć układu, w którym nie ma tłumienia (p = 0) jest nieskończenie wielka, natomiast gdy

■ Jeżeli jest spełniony warunek p «a>₍j to mówimy, ze tłumienie jest słabe. W takim przypadku to = «.>_G i T= /„ =    ■ Energię całkowitą drgań, która

ogolnic dla drgań tłumionych jest dość skomplikowaną funkcją czasu, możemy w przpadku słabego tłumienia zapisać w postaci

_F _ m<o²i4(/)² _ ^wt°~^o _2p/

/i =    2    ~    2 ^e

Otrzymany wzór na energię jest podobny do wzoru dla przypadku drgań sw-obodnych (patrz punkt 44) Różnica polega jedynie na tym, żc w przypadku drgań swobodnych amplituda mc zależy od czasu

47. Drgania tłumione

równanie różniczkowe drgań tłumionych

Ć^ZX

dLv

współczynnik thimicnia d współczynnik oporu ośrodka

faza początkową drgania tłumionego

1 częstość drgań własnych

nr

*>0 = v»

k - współczynnik proporcjonalności między siłą harmoniczną a wychyleniem

amplituda drgań thimionyc

x = ^(/)COS(CO/+ (p

częstość drgań tłumionych

-^-a-r	1 r “-7 II
A(t) = /Jo^e = ]	[ a> = v'q>5 - p^2 |

'» czas relaksacji a czas. po którym amplituda zmnleje C raz* t - p

amplituda drgań < w chwili / = 0