skrypt wzory i prawa z objasnieniami47

92 J ¹ Małe drgania ■ Jeżeli energia potencjalna układu, którego ruch opisany jest zmienną x ma minimum w punkcie x₀. to ruch układu wokół położenia równowagi w przypadku małych wychyleń ma zawsze postać drgań harmonicznych Energia potencjalna jest wtedy kwadratową funkcją zmiennej x, siła jest proporcjonalna do wychylenia i skierowana zawsze do położenia równowagi.

■ Wzór na energię potencjalną w przybliżeniu harmonicznym wynika z rozwinięcia funkcji F._p = E_p(x) w szereg potęgowy wokół punktu

£p(x) = £p(a:₀) +^|x=jr₀(x-x₀)-ł-y^7|j:=jf₀(x-.ro)" +...

Ponieważ funkcja £(*) ma minimum w punkcie x,. drugi wyraz rozwinięcia równy jest zeru. Dla małych wychyleń z położenia równowagi (.małych drgań) można odrzucić wszystkie człony rozwinięcia o wykładnikach większych niz dwa Porównując otrzymane w taki sposób wyrażenie

I d²£n I    ")

£p(x) = £p(xo) + 7^j~|x=u:₀(x-Xo)*"

ze wzorem na energię potencjalną drgań harmonicznych

r- _ ty^X-^X0)²

^bP~ -2-

możemy wyznaczyć stałą k

+ C

x=xo

r l^gp ' 2 d*²

■    Jeżeli początek układu współrzędnych wybierzemy tak. że ^=0. to wzory na energię potencjalną i siłę przyjmą standardową uproszczoną postać

£_P=*jr- r=-kx

■    Jeżeli drgania nie są małe, to w rozwinięciu funkcji £(x) w' szereg potęgowy należy uwzględnić kolejne wyrazy. Oczywiście wtedy ruch układu przestaje być ruchem harmonicznym

Drgania harmoniczne

CS

45. Przybliżenie małych drgań

, położenie równowagi

Ep(*o)

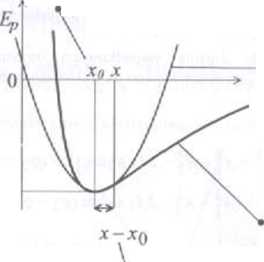
i minimalna wartość ^ wychylenie układu energii potencjalnej    z położenia równowagi

E_p = E_p(x o) +    -jr₀)²

♦ zależność energii potencjalnej od wychylenia dla drgań harmonicznych

Ep = E_p(x)

rzeczywista zależność energii potencjalnej od wychylenia

Ep(x) = Ep{x₀) +\k(x- x₀)²

energia potencjalna * dla małych wychyleń z położenia równowagi

i

współczynnik proporcjonalności między siłą a wychyleniem z położenia równowagi