skrypt wzory i prawa z objasnieniami05

8

Prędkość

■ Tor jest to krzywa opisywana w przestrzeni przez poruszający się punkt W zależności od kształtu toru rozróżnia się prostoliniowy i krzywoliniowy ruch punktu Ruch punktu nazy wa się płaski, gdy wszystkie odcinki jego toru lezą w jednej płaszczyźnie ■ Równanie toru we współrzędnych kartezjańskich ma ogólną postać

np. dla ruchu po okręgu o promieniu R i środku w początku układu współrzędnych równanie toru jest następujące:

*² + y²=*² ,

czyli

■    Prędkość (prędkość chwilowa) jest to wielkość wektorowa v równa pierwszej pochodnej wektora położenia r poruszającego się punktu względem czasu t.

Z definicji prędkości wynika, że

= ?d/,

zatem wektor prędkości jest skierowany zawsze wzdłuż stycznej do toru w' kierunku ruchu punktu

■    Długość drogi s jest to suma wszystkich odcinków toru, przebytych przez punkt w rozpatrywanym przedziale czasu

j =    = f \d~r\ = f-tU = f |"v U= jV

* i¹ 1 U * t_A\ I ij

■    Zauważmy, że jeśli ciało porusza się po tarze ze stałą prękością v, to prędkość średnia równa jest tej prędkości i zachodzi związek

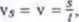
gdzie s jest drogą przebytą przez ciało w czasie t.

2. Prędkość

Kinematyka 9

elementarne przesunięcie d i * = \dt

!\fr =dy

- druga przebyta przez cząstkę ud chwili .* do chwili f -d.'

wektor położenia cząstki w chwili /

początek układu współrzędny

wektor położenia cząstki w chwili t+ d/

| prędkość cząstki w chwili t

► lor ruchu cząstki

^s B

wektor prędkości

droga przebyta przez cząstkę w przedziale czasu ftĄdu)

V =

d_r_

d/

wektor położenia cząstki r - r [!)

2.1 Prędkość średnia

prędkość średnia poruszającej się cząstki w przedziale czasu (t_Ar i^)

/

droga przebyła przez cząstkę ud chwili t_A do chwili Ig