skrypt wzory i prawa z objasnieniami23

44

Pole grawitacyjne

■ Energia potencjalna w polu grawitacyjnym jest to praca, jaką wykona siła grawitacji przy przesunięciu ciała z danego punktu pola do nieskończoności (czyli we wzorze w punkcie 16 1 wystarczy przyjąć r# -+co i otrzymujemy wzór z punktu 17). Przy takim wyborze sposobu liczenia energia potencjalna nieskończenie daleko od źródła pola (tam. gdzie siła grawitacji przestaje działać) wynosi zero (poziom zerowy energii potencjalnej znajduje się w nieskończoności). Opisując pole grawitacyjne przy powierzchni Ziemi poziom zerowy energii potencjalnej wybieramy inaczej, np. powierzchnię Ziemi.

■    Po zdefiniowaniu energii potencjalnej pracę sił pola można przedstawić następująco

^WA->B ~ Ep(^rA) ~ Ep(^rB)³ ”

Przy ruchu swobodnego ciała w polu grawitacyjnymi wykonanie przez pole powyższej pracy spowoduje zmianę energii kinetycznej ciała

Przyrównując do siebie powyższe rówmama otrzymujemy zasadę zachowania całkowitej energii mechanicznej, gdyż:

AEfr +    = 0

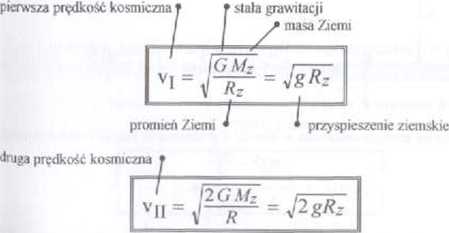
■    Pierwsza prędkość kosmiczna v, to prędkość z jaką należy wystrzelić ciało z powierzchni Ziemi, aby me spadło ono z powrotem na Ziemię, a zaczęło krążyć po orbicie kołowej o promieniu zbliżonym do promienia Ziemi R, Prędkość tę uzyskamy przyrównując siłę odśrodkową (patrz punkt 11.2) działającą na satelitę o masie m na orbicie kołowej o promieniu R, i siłę przyciągania grawitacyjnego, której źródłem jest Ziemia o masie Ki. Otrzymujemy równanie

""i    .. «W;

■sr^=Gir

z którego wyznaczamy pierwszą prędkość kosmiczną

^{V| a = = 7 9 km/s}'

■    Druga prędkość kosmiczna to tzw prędkość ucieczki. Jest to najmniejsza prędkość z jaką należy wystrzelić rakietę na powierzchni Ziemi, aby uciekła ona z pola grawitacji Ziemi Energia całkowita tej rakiety poza polem grawitacji Ziemi ma wynosić zero Energia całkowita jest zachowana, a więc musi się zerować i na powierzchni Ziemi Korzystając z oznaczeń wyżej

Gm\-ł~ wvf|

wprowadzonych otrzymamy równanie. —= 0. z którego wyznaczamy drugą prędkość kosmiczną.

vjj =    =

Dynamika punktu materialnego 45

17. Energia potencjalna w polu grawitacyjnym

stała grawitacji \    ] inasa źródła pola grawitacyjnego

U=

Mm

EpA=-G_T7

energia potencjalna ciała o masie m w punkcie A

:iała ^    i

odległość punktu A od źródła poła grawitacyjnego ( w przypadku kuł odległość między ich środkami)

18. Zasada zachowania energii w polu grawitacyjnym

całkowita energia mechaniczna

ciała poruszającego się w polu grawitacyjnym

E_c = E_u + E_pA = E_kB + E_pB = const

energia kinetyczna w punkcie A, gdzie ciało posiada prędkość \ą

n

energia potencjalna

w punkcie A odległym o r_A od źródła poła

_ r* Mm

U

19. Prędkości kosmiczne