skrypt wzory i prawa z objasnieniami58

114 Zasady zachowania energii i pędu

■ Musimy pamiętać, że w mechanice relatywistycznej do opisu zderzeń i rozpadów cząstek zawsze stosujemy dwie zasady zachowania zasadę zachowania pędu i zasadę zachowania energii ( W mechanice klasycznej w przypadku zderzeń niespręźystych stosuje się tylko zasadę zachowania pędu i Oczywiście pod nazwą energii w mechanice relatywistycznej kryje się całkowita energia cząstek uwzględniająca zarowno ich energie kinetyczne jak i energie spoczynkowe.

■ Opis zderzenia dwóch cząstek przedstawiony w 55 1, w którym po zderzeniu mamy nadal dwie cząstki, tylko o innych pędach i energiach, jest przypadkiem szczególnym Ogólnie, podczas zderzenia dwóch cząstek mo2e powstać bądź jedna, bądź więcej mź dwie cząstki Oprócz tego część energii albo nawet cała energia całkowita cząstek biorących udział w zderzeniu może zostać- wyemitowana w postaci bezmasowych ( czyli o zerowej masie spoczynkowej) cząstek - fotonów Przykładem może być zderzenie elektronu i pozytonu Jest to przykład anihilacji cząstek, gdyż z dwóch cząstek

posiadających masę spoczynkową h    powstają w wyniku zderzenia fotony -

foton cząstki nic posiadające masy -fi spoczynkowej Zakładając, jak to pokazano na rysunku, że pędy cząstek elektron ,'    pozyton biorących udział w zderzeniu są takie

j-_0|on    same co do wartości a różnią się jedynie

zwrotem, po anihilacji powstałe fotony również muszą mieć jednakowe wartości

pędów P(=j. a co za tym idzie, jednakowe energie równe fiv. Z zasady zachowania energii, uwzględniając, że masa pozytonu równa jest masie elektronu m_e otrzymujemy

2cjrtiec² +p² = 2/iv

a stąd

cJm%c²+p² V= h

Jeżeli pędy elektronu i pozytonu są równe zeru ( bądź bliskie zera), to

v-2££i

^v" h

Podstawiając m_e =9.1 10 ^ł,kg. c = 3 10* m/s. h 64 10'^uJs, otrzymujemy v = 1 2 10*° s'¹ Odpowiadająca długość fali X = c/v wynosi X= 2.5 10‘^,Jm ~ 0.025 angstrema Tak więc podczas anihilacji elektronu i pozytonu powstaje promieniowanie elektromagnetyczne odpowiadające bardzo twardemu promieniowaniu gamma

[

Mechanika relatywistyczna

115

55. Zderzenia relatywistyczne

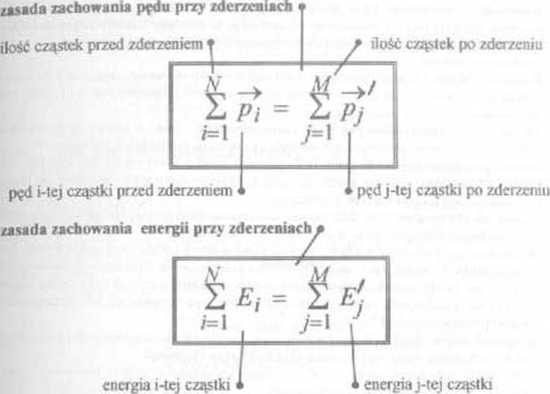
pr/cd zderzeniem

po zdcr/cniu

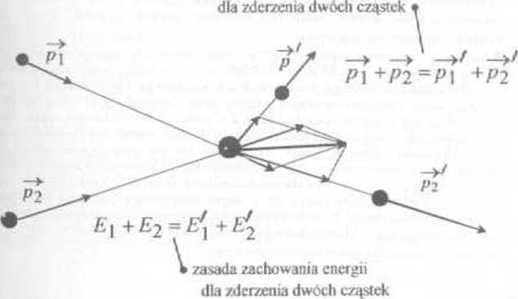
55.1 Zderzenia dwóch cząstek

zasada zachowania pędu