skrypt wzory i prawa z objasnieniami45

88

Wahadło fizyczne

■ Równanie różniczkowe ruchu wahadła fizycznego otrzymujemy z drugiej zasady dynamiki ruchu obrotowego /e M . gdzie / jest momentem bezwładności bryły sztywnej względem osi obrotu, czyli osi przechodzącej przez punkt zawieszenia i prostopadłej do płaszczyzny wahań wahadła, a

e = ^ jest jego przyspieszeniem kątowym. Przy założeniu. Ze wychylenia dr

« z położenia równowagi są niewielkie, możemy przyjąć, ze ( podobnie jak w przypadku wahadła matematycznego)

A/ = -mg! sin a s - mglu.

Po przekształceniach otrzymujemy równanie różniczkowe drgań harmonicznych wahadła fizycznego w postaci

+ —j-ct = 0. di² 1

Porównując to równanie z ogólnym równaniem drgań opisywanych zmienną kątową a

^ + <o²a= 0 di²

fmgF    _ j J

otrzymujemy. Ze o = y— , a / =    .

■ Należy pamiętać, ze / występujące we wzorze na okres drgań wahadła fizycznego jest momentem bezwładności wahadła względem osi obrotu przechodzącej przez punkt zawieszenia, a nie przez środek masy. Bardzo często dla brył symetrycznych, takich jak kula, walec itp. znamy ten ostatni moment bezwładności (oznaczmy go przez /„). Wtenczas, aby otrzymać 1 korzystamy z twierdzenia Steinem

/ = /„ + mP

■ Można pokazać, że wahadło matematyczne jest szczególnym przypadkiem wahadła fizycznego. Podstawiając we wzorze na okres drgań wahadła fizycznego I = ml² otrzymujemy wzór na okres drgań wahadła matematycznego:

l

f ml²

43. Wahadło fizyczne

odległość środka masy wahadła od punktu zawieszenia

punkt zawieszenia (oś obrotu >

Mt wychylenia wahadła z położenia równowagi

gsina

^ składowa siły ciężkości dająca moment zwTotny

M - mglsin a

masa wahadła fizycznego

siła ciężkość i przyłożona do środka masy ciała

zależność wychylenia wahadła fizycznego z położenia równowagi od czasu, dla małych wychyleń (sina = a)

a = a_m cos(od? +

i

amplituda drgań wahadła fizycznego

⁴ faza początkową drgań częstość drgań wahadła

43.1 Okres drgań wahadła fizycznego

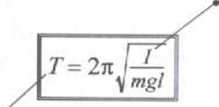
moment bezwładności względem osi obrotu

okres drgań ■ wahadła fizycznego