skrypt wzory i prawa z objasnieniami42

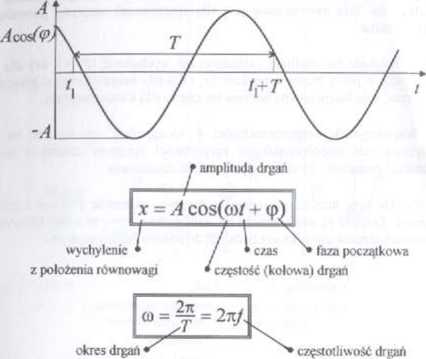
82 Równanie drgań harmonicznych

■    W równaniu drgań harmonicznych przyjęto, Ze drgania zachodzą wokół położenia równowagi x = 0 Je2eli położenie równowagi jest dla x = jr„, to w równaniu drgań zastępujemy x przez x - x,

■    Wielkość x w równaniu drgań oznacza zmienną liniową opisującą ruch drgający. Nie musi to być koniecznie ruch zachodzący wzdłuż prostej, ale np po tuku, jak ruch punktu materialnego w wahadle matematycznym. W przypadku ruchu po luku wygodniej jest opisywać ruch drgający przy pomocy zmiennej kątowej a (wahadło matematyczne i fizyczne ). Równanie drgań ma wtenczas postać

a=o.„ cos (ror+o) ,

gdzie a„ oznacza wartość maksymalnego kąta wychylenia z położenia równowagi

■    Równanie ruchu drgającego możemy również zapisać poprzez funkcję sinus jako

x = zfsin (cof+$).

Różnica pomiędzy sposobami zapisania równania związana jest z wartością fazy początkowej Jeżeli chcemy przejść, przy opisie ruchu harmonicznego, od funkcji typu sinus, do funkcji typu cosmus, należy podstawić $ = 9 + "

■    Prędkość i przyspieszeoie w ruchu drgającym otrzymujemy na podstawie wzorów

v = & = -uA sin(cof + <p)

a = ^    ~ = -a^A cosfcoi + o) = -o>-jr

At fal

W powyższych wzorach o/ljcst maksymalną wartością prędkości, a <a‘A maksymalną wartością przyspieszenia

■    Wzór na silę w ruchu drgającym, zgodnie z drugą zasadą dynamiki, otrzymujemy z następujących relacji:

F = ma = -m<j)~x = -kx z czego wynika, że moi² = Ir, czyli (o = ^

-

40.Drgania harmoniczne

F = -kx

*    V.

siła harmoniczna •    • współczynnik proporcjonalności

między siłą a wychyleniem

40.1    Siła w ruchu harmonicznym

40.2    Równanie różniczkowe drgań harmonicznych

masa drgającego ciała