skrypt wzory i prawa z objasnieniami50

98

Składanie drgań

■ W naszym przypadku częstości drgań wzajemnie prostopadłych są takie same Jeżeli częstości tc są różne, to tor ruchu wypadkowego jest dość złożoną krzywą. W przypadku, gdy stosunek częstości jest liczbą wymierną tj równy jest stosunkowi liczb całkowitych, tor będzie krzywą zamkniętą, tzw. figurą Lissajous. Poniżej przedstawiono na rysunku dwa przykłady złożenia dwóch drgań prostopadłych takich. Ze drganie w kierunku osi OY ma częstość dwukrotnie większą niż w kierunku osi OX. Różnica między wynikiem złożenia drgań związana jest z różnicą przesunięć fazowych między' drganiami składowymi

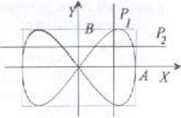
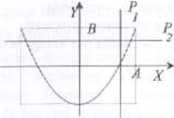
x = Acos(ot) y= Bcos[2tat +    r = .4cos(a)/} y = /łcos(2caf)

W zależności od różnicy faz początkowych obydwu drgań otrzymujemy różne kształty' figur Lissajous Wielkością niezmienną, jak to pokazano na rysunku, jest stosunek liczby przecięć figury Lissajous z prostą pionową P_x do liczby przecięć z prostą poziomą P_:. Stosunek ten jest równy stosunkowi częstości drgania w- kierunku osi OX do czystości drgania w kierunku osi OY (w naszym przypadku wynosi |) ■ Najprostszym sposobem obserwacji krzywych Lissajous jest obserwacja toru plamki na ekranie oscyloskopu, do którego okładek X i Y przyłożono sygnały napięciowe o tych samych luh różnych częstościach W pierwszym przypadku zaobserwujemy elipsę a w pozostałych jedną z krzywych Lissajous

Drgania harmoniczne 99

46.3 Składanie drgań prostopadłych

wychylenie wzdłuż osi OY ^ J

yA y= 5cos(a)/ + cp^

amplituda drgania w kierunku osi OY

przesunięcie fazowe między drganiami

jednakowa częstość dla obydwu drgań

Tlt

A cos (co/)

X amplituda drgania w kierunku osi OX

ruchu cząstki uczestniczącej    • wychylenie w kierunku osi OX

w dwóch wzajemnie prostopadłych drganiach

prosta o równaniu    prosta o równaniu elipsa, której osie

y=^ x    y=    pokrywają się z osiami

układu współrzędnych