skrypt wzory i prawa z objasnieniami46

90 Energia drgań harmonicznych
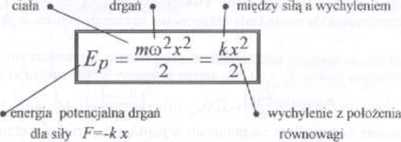
■ Wzór na energię potencjalną drgań harmonicznych otrzymujemy z ogólnego związku między energią potencjalną a siłą, którą w tym przypadku jest siła harmoniczna W przypadku jednowymiarowym mamy
£p = -jFdx = j£(*-XQ)dxr = + C
gdzie C jest dowolną stałą, którą możemy przyjąć równą zeru. Gdy położenie równowagi xq = 0, to otrzymamy wzór z punktu 44
p - fsŁ
■ Biorąc pod uwagę wzór na siłę harmoniczną, F- -la , energię potencjalną drgań harmonicznych można również wyrazić w' postaci r _kx2 _ (**)2 _ F2
kp-~-ir-2k
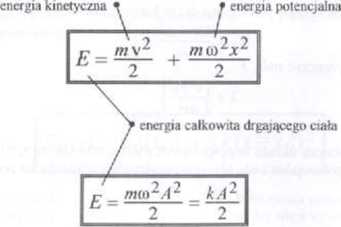
■ Ponieważ siła harmoniczna jest siłą potencjalną, dlatego tez spełniona jest zasada zachowania energii mechanicznej dla ciała wykonującego drgania harmoniczne. Czyli energia całkowita E jest sumą energii kinetycznej oraz energii potencjalnej i wynosi
= Wfl>^4~[( cos2(<iW + <p) +sin2(to/ + <p)] =
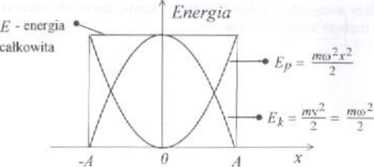
Zauważmy, że energia całkowita jest równa maksymalnej energii potencjalnej (do wzoru na energię potencjalną podstawiamy x A. energia kinetyczna jest wtedy równa zeru), a także maksymalnej energii kinetycznej (do wzoru na energię kinetyczną podstawiamy v=vmax =(oA, energia potencjalna jest wtedy równa zeru)
44.Energia potencjalna drgań harmonicznych
masa drgającego częstość (kołowa) współczynnik proporcjonalności
44.1 Zasada zachowania całkowitej energii mechanicznej drgań
Wyszukiwarka
Podobne podstrony:
skrypt wzory i prawa z objasnieniami42 82 Równanie drgań harmonicznych ■ W równani
skrypt wzory i prawa z objasnieniami49 96 Składanie drgań ■ Przy składaniu drgań o
skrypt wzory i prawa z objasnieniami48 94Składanie drgań ■ Reprezentacja drgania h
skrypt wzory i prawa z objasnieniami50 ■ W naszym przypadku częstości drgań wzajemnie prostopadłych
skrypt wzory i prawa z objasnieniami58 114 Zasady zachowania energii i pędu ■ Musimy pamiętać, że w
skrypt wzory i prawa z objasnieniami21 40 Moc i energia kinetyczna ■ Wychodząc z definicji mocy P-ŚE
skrypt wzory i prawa z objasnieniami23 44Pole grawitacyjne ■ Energia potencjalna w polu grawitacyjny
skrypt wzory i prawa z objasnieniami51 100 Drgania tłumione ■ Równanie różniczkowe drgań tłumionych
skrypt wzory i prawa z objasnieniami52 102 Drgania wymuszone ■ Równanie różniczkowe drgań wymuszonyc
skrypt wzory i prawa z objasnieniami31 60 Zderzania sprężyste i niesprężyste ■ W z
skrypt wzory i prawa z objasnieniami43 Siła sprężysta ■ Wzór na siłę harmoniczną powodującą drgania,
skrypt wzory i prawa z objasnieniami47 92 J 1 Małe drgania ■ Jeżeli energia potencjalna układu, któr
skrypt wzory i prawa z objasnieniami49 96Składanie drgań ■ Przy składaniu drgań o różnych częstościa
skrypt wzory i prawa z objasnieniami50 98Składanie drgań ■ W naszym przypadku częstości drgań wzajem
skrypt wzory i prawa z objasnieniami58 114 Zasady zachowania energii i pędu ■ Musimy pamiętać, że w
skrypt wzory i prawa z objasnieniami03 4 Układy współrzędnych ■ Układem odniesienia nazywamy ciało,
skrypt wzory i prawa z objasnieniami05 8 Prędkość ■ Tor jest to krzywa opisywana w przestrzeni przez
więcej podobnych podstron