skrypt wzory i prawa z objasnieniami49

96 Składanie drgań

■    Przy składaniu drgań o różnych częstościach przyjmujemy, że faza początkowa obydwu drgań jest równa zeru. Nie zmienia to ogólności rozważań, gdyż jeżeli drgania mają różne częstości, to różnica ich faz cały czas ulega zmianie, a co za tym idzie wystarczy jako chwilę początową przyjąć tę, w której oba drgania mają maksymalne wychylenie o tym samym zwrocie

■    Dudnienia. Jeżeli spełniony jest warunek <02-a>i «    +(°2« ^{to wc}

wzorze na drganie wypadkowe x czynnik w nawiasie kwadratowym zmienia się w funkcji czasu powoli w porównaniu z czynnikiem cos(—Pozwala to nam traktować drganie wypadkowe jako drganie harmoniczne o częstości <n = i o zmiennej w czasie amplitudzie. Za zmienną w czasie amplitudę uważamy moduł z wyrażenia w nawiasie kwadratowym. Moduł wprowadzamy dlatego, ze amplituda musi być wielkością dodatnią. Tak zdefiniowana amplituda zmienia się w czasie okresowo z częstością i*j = u>2 a>i (częstość dudnień). Zauważmy, że nie jest to częstość funkcji cosinus w nawiasie kwadratowym, lecz częstość dwukrotnie większa, gdyż w definicji amplitudy występuje moduł funkcji cosinus.

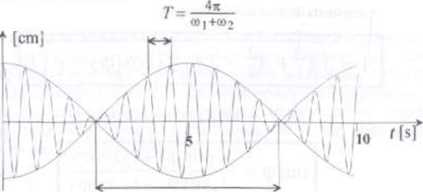
■    Poniżej przedstawiamy przykład złożenia drgań, który może być traktowany jako przykład dudnień. Załóżmy, że składamy dwa drgania równoległe o jednakowych amplitudach .4-1 cm i częstościach kołowych równych coj = 9.4s^-1,012 = I0.6s“*. Zgodnie ze wzorem z punktu 46 2 otrzymamy drganie wypadkowe x= 2 cos(0.6/) cos(10/) Poniższy rysunek przedstawia wykres drgania wypadkowego z zaznaczeniem efektu dudnień

X

2

Drgania harmoniczne

46.2 Składanie drgań równoległych o różnych częstościach

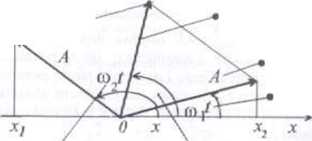
x| =/łcos(coj/)

częstość ł pierwszego drgania

w^ość wychylenia

z położenia równowagi

dla drgania pierwszego w chwali t

97

*2 =^cos(a)20

\ częstość drugiego drgania (załóżmy, że ti₂ >a>i)

amplituda drgali, jednakowa dla drgania pierwszego i drugiego

amplituda drugiego drgania t

amplituda drgania wypadkowego

-T

amplituda pierwszego drgania faza pierwszego drgania

faza drugiego drgania * faza drgania wypadkowego^ —^J i

X =	’ (Ot-O) i 24 cos ^—z—	-)1	cosf^r^2/)

drganie wypadkowe x = x\ +