skrypt wzory i prawa z objasnieniami10

Rzut pionowy

■ Rzuty ciała przy powierzchni Ziemi przy założeniu jednorodności pola grawitacyjnego (patrz punkt 20) i zaniedbaniu sił oporu powietrza są przykładem ruchu jednostajnie zmiennego (patrz komentarz do punkt 5). W tym przypadku stale przyspieszenie ciała jest równe przyspieszeniu ziemskiemu a ~g W zależności od kierunku wektora prędkości początkowej wyrzuconego ciała względem wektora g rozróżniamy następujące rodzaje rzutów rzut pionowy fvjj|l?)» rzut poziomy

( vo 1 g ) oraz rzut ukośny (dowolny kąt między wektorami v₀ i g) W prz>padku. gdy prędkość początkowa jest równa zeru ruch ciała nazywamy spadkiem swobodnym ■ Możemy rozróżnić rzut pionowy do góry i rzut pionowy w dół W rzucie pionowym do góry prędkość początkowa ma zwrot przeciwny do zwrotu przyspieszenia ziemskiego, natomiast w rzucie w dół zwroty prędkości początkowej i przyspieszenia ziemskiego są zgodne.

Jeżeli dla rzutu pionowego do góry przyjmiemy, że wektor prędkości początkowej o ma zwrot zgodny /. kierunkiem osi OY, to wtedy wektor przyspieszenia, którego wartość wynosi g. jest skierowany przeciwnie niż kierunek osi OY. W pewnej chwili t_l( ciało wyrzucone do góry osiąga wysokość maksymalną II i zawraca. Czas i_ff potrzebny na osiągnięcie wysokości maksymalnej // wyznacza się z warunku Vy(Jn) - v₀ - gin - 0

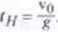
i wynosi on

Z kolei wartość H wyznaczamy z równania:

2

= ^v0 *H 2^gtH ⁼ 2i

Całkowity czas U potrzebny do powrotu ciała do położenia początkowego wyznaczymy z warunku >{/) = \₀l - jgt² = 0. Otrzymujemy dwa

2v₀ ,

rozwiązania /| = 0 (odpowiada chwili początkowej) i 12 = tc = —(czyli całkowity czas rzutu).

6. Rzuty

6.1 Rzut pionowy

Kinematyka 19

położenie ciała wyrzuconego pionowo do góry z powierzchni Ziemi z prędkością początkową v₀ w pewnej dowolnej chwili czasu t.

maksymalna wysokość r/utu¹

współrzędna prędkości ciato Vy w dowolnej chwili i

^v> =^v<>

prędkość początkowa • rudiu ciała

położenie początkowe -

^v0

" O

y=\₀t-\gi²

przyspieszenie ziemskie

P(y) czas potrzebny na osiągnięcie maksymalnej wysokości H

►

X

położenie ciała w jiewnej dowolnej chwili / rzuconego pionowo w dół z wysokości h nad powier/cłmią Ziemi z prędkością początkową v_;;

i

współrzędna prędkości ciała w dowolnej chwili:

położenie początkowe ciała

prędkość początkowa ciała

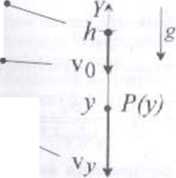
j y=li- v₀/-|gf²