skrypt wzory i prawa z objasnieniami38

74

Ruch obrotowy ciała

■ Jak wynika z własności iloczynu wektorowego dwóch wektorów, wektor —)

momentu siły M jest prostopadły do płaszczyzny, w której lezą wektory _^ —>

r i F Jego zwrot jest zgodny z kierunkiem ruchu postępowego śruby prawoskrętnej podczas jej wkręcania od wektora ~r do F

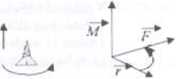
Jeżeli są dane współrzędne wektorów siły i promienia wodzącego, to wektor momentu siły znajdujemy licząc iloczyn wektorowy za pomocą metody —►    —>

wyznacznika Np., niech F = (0.0,5]N i r=[0, l.ljm, to

_>

M=rxF=

= 5 / = [5,0,0] Nm

■ Często wygodniej jest wyznaczyć wartość momentu siły wykorzystując pojęcie ramienia działania siły. Ramię działania siły to odległość / prostej na której leży wektor siły od punktu O. względem którego moment jest liczony Sposób wyznaczenia ramienia działania siły pokazuje rysunek:

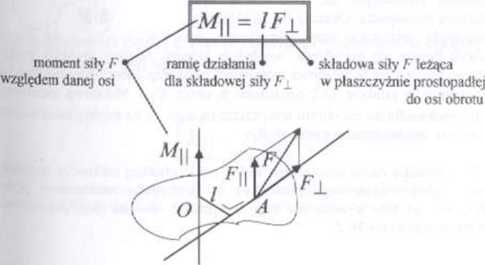
■ Wyznaczając wartość momentu siły względem jakiegoś punktu leżącego na osi obrotu, otrzymamy wektor, którego składowa równoległa do osi nie będzie zalezeć od wyboru punktu, względem którego liczyliśmy moment siły Otrzymaną w ten sposób składową momentu siły nazywamy momentem siły względem danej osi W zadaniach najczęściej jest mowa właśnie o momencie siły względem danej osi obrotu, gdyż wielkość ta wpływa na ruch obrotowy ciała. W praktyce wyznaczamy moment siły' F względem danej osi rozkładając wektor siły na składową równoległą do osi F||. która me daje przyczynku do momentu siły względem tej osi, i składową leżącą w płaszczyźnie prostopadłej do osi F±. Następnie składową prostopadłą

mnożymy przez ramię działania siły. czyli w tym przypadku, odległość —>

prostej, na której leży wektor F od osi obrotu

Dynamika układu punktów materialnych

75

35. Moment siły

35.1 Moment siły względem danego punktu

M = r x F

wektor momentu siły względem danego punktu O

wektor łączący punkty O i A

rr

siła przyłożona w pewnym punkcie A do ciała

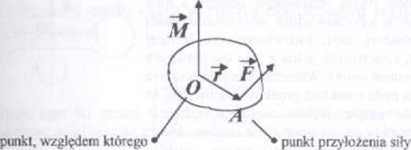
liczony jest moment siły    wprawiającej ciało w ruch

obrotowy

35.2 Moment siły względem danej osi