skrypt wzory i prawa z objasnieniami35

68

Moment bezwładności

■    Należy pamiętać o tym, że moment bezwładności ciała wyznaczamy zawsze względem pewnej osi Zmiana osi spowoduje zmianę wartości momentu bezwładności (patrz tez twierdzenie Steinem w punkcie 32).

■    \1ozna powiedzieć, ze moment bezwładności ciała jest dla ruchu obrotowego tym, czym masa ciała dla ruchu postępowego Im większy moment bezwładności, tym trudniej jest wprawić ciało w ruch obrotowy Przytaczając tę analogię należy pamiętać o jednej istotnej różnicy - dla danego ciała masa jest wielkością wyznaczona jednoznacznie, natomiast moment bezwładności zależy nie tylko od danego ciała, ale również od wyboru osi obrotu

■    Występujący w całce po objętości nieskończenie mały element objętości wyraża się dla współrzędnych kartezjańskich zależnością dV- dlrdj-dz W przypadku współrzędnych cylindrycznych p, cp, i z zależność ta jest następująca dJ^/= p dpdq> dr, natomiast dla współrzędnych sferycznych r, 8 i <p -

ÓV= r² sin 3 drd3d<p

■    Najczęściej w- zadaniach będziemy liczyć moment bezwładności dla ciała jednorodnego Czyli gęstość ciała p = p(jc, y, z) = consl. i można wyłączyć ją przed znak całki, a następnie wyeliminować ze wzoru końcowego podstawiając p = mlV.

■    Moment bezwładności jakiegoś złożjonego ciała, np kuli w połowie wykonanej ze stali, a w połowie wykonanej z miedzi, wyznaczymy sumując momenty bezwładności części składowych (oczywiście wszystkie momenty bezwładności muszą być liczone względem tej samej osi).

■    Moment bezwładności jednorodnego ciała wydrążonego najszybciej można znaleźć licząc moment bezwładności ciała złożonego z dwóch części składowych ciała bez wydrążenia i ciała o kształcie wydrążenia. Oczywiście laka procedura będzie miała sens, gdy momenty bezwładności części składowych są znane. Licząc więc moment bezwładności ciała / wydrążeniem, sumujemy momenty bezwładności części składowych, przypisując ciału o kształcie wydrążenia ujemną gęstość (wszystkie momenty bezwładności muszą być Uczone względem tej samej osi) Inaczej mówiąc, należy od momentu bezwładności dla całego ciała odjąć moment bezwładności dla wydrążenia.

Dynamika układu punktów materialnych

31. Moment bezwładności ciała względem danej osi

gęstość ciała f->\

symboliczny zapis    całka po objętości

całki po całym ciele    V ciała

o masie M

31.1 Moment bezwładności w kartezjańskim układzie współrzędnych względem osi OZ

69

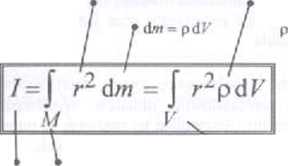
moment bezwładność dała względem danej osi obrotu

r - odległość elementu masy dw» od osi obrotu

-10

V

kwadrat odległości od osi obrotu

r²-*²**²

+ >'² j p(x,y,z)dxdydz

tziZZZT -L

moment bezwładnoścN liczony względem osi 07 jako osi obrotu

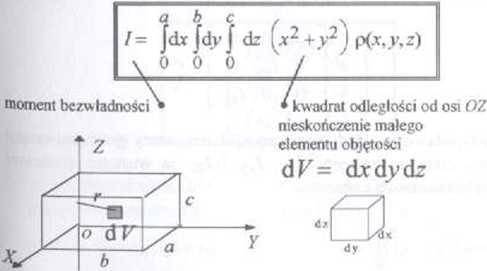
element objętości w kartezjańskim układzie współrzędnych

dr=dtdvtL-

31.2 Moment bezwładności prostopadłościanu względem osi OZ