skrypt wzory i prawa z objasnieniami37

72

Moment bezwładności

■ Moment bezwładności punktu matenalnego o masie m oddalonego o </od osi obrotu wynosi / = md~

■ Moment bezwładności cienkościennej obręczy o masie M i promieniu R względem osi symetrii obręczy można wyznaczyć bez liczenia całki z punktu 31. gdyż cała masa obręczy znajduje się w tej samej odległości od osi obrotu Otrzymamy dla tego przypadku / = XfR~.

■ Zauważmy, że podany moment bezwładności walca nic zależy od jego wysokości Tak więc moment bezwładności tarczy (walec o bardzo małej wysokości) wyniesie również l=MR², gdzie M jest masą jednorodnej tarczy', a R jej promieniem.

■ Znając moment bezwładności prostopadłościanu łatwo przejść do momentu bezwładności dla jednorodnego sześcianu przyjmując, że a^b. Otrzymamy wtedy moment bezwładności sześcianu względem osi prostopadłej do jego boków i przechodzącej przez jego środek:

/ = i Ma¹.

O

■ Momenty' bezwładności podane w punkcie 34 są momentami bezwładności brył względem ich osi symetrii Można je wykorzystać do obliczania momentów bezwładności tych brył względem dowolnych innych osi obrotu równoległych do osi symetrii. Należy w tym celu skorzystać z twierdzenia Steinem {patrz punkt 32). Przykładowo, moment bezwładności dla pręta względem osi do mego prostopadłej i przechodzącej przez jego koniec wyniesie:

+ A.(£;²=iM²,

gdyż w tym przypadku odległość między osiami d=lfl

Dynamika układu punktów materialnych

73

34. Momenty bezwładności niektórych brył

M

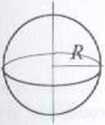
i=\mr²

--I

• moment bezwładności jednorodnej kuli o promieniu R i masie if względem osi przechodzącej przez jej środek

i=\mr² j|

moment bezwładności jednorodnego walca o promieniu podstawy R i masie M względem jego osi symetrii

M

I = ±Ad(a² + b²)

^ moment bezwładności jednorodnego prostopadłościanu o podstawie o bokach a i b i masie M względem osi przechodzącej przez środki podstaw

o

i

• moment bezwładności jednorodnego cienkiego pręta o długości i i masie M względem osi prostopadłej do pręta i przechodzącej przez jego środek

Mi²