skrypt wzory i prawa z objasnieniami56

110

Transformacje prędkości

■ Musimy pamiętać, te podane wzory transformacyjne prędkości wyprowadzono przy założeniu, że układ K' porusza się w prawo tj. zgodnie z osią OX Gdy układ K porusza się w lewo to w podanych wzorach należy zamienić v_t na -v₀.

■ Jeżeli wzajemna prędkość poruszania się układów jest dużo mniejsza od prędkości światła, to we wzorach transformacyjnych można pominąć

(■£) *^w porównaniu z jedynką i otrzymujemy: v_r=vx+v₀,

^vż^=v> • ^v- =^vr Są to wzory transformacyjne prędkości w przybliżeniu klasycznym wynikające z transformacji Galileusza ■ Oprócz szczególnego przypadku składania prędkości, gdy v' II v₀można

—►    _f

rozważyć przypadek, rzadziej spotykany w zadaniach, taki, że v^ł _l v₀. Załóżmy, że prędkość jest skierowana wzdłuż osi OT układu K\ czyli v’ = [0,v\0]. W tym przypadku w układzie A' prędkość ma dwie niezerowe składowe, które wynoszą

Vx = vp

Vy = v'Jl-(ir)

■ Jeżeli cząstką poruszającą się w układzie K jest foton, to wartość jego prędkości wynosi c. Obliczmy prędkość v fotonu w układzie K w dwóch przypadkach

l° Foton ma kierunek i zwrot tj porusza się w stronę dodatnich wartości osi OX . Wtedy

c+v o    c+vq

^v" ^C

^{ęl C}    -»

T Foton porusza się w kierunku prostopadłym do v₀ wzdłuż osi OT Wtedy___

v= = jv'o-(v₀/O² j =

W obydwu przypadkach stwierdzamy, ze prędkość fotonu co do wartości jest taka sama w obydwu układach odniesienia.

Mechanika relatywistyczna

111

52. Relatywistyczna transformacja prędkości

układ K' poruszający się z prędkością Vq

prędkość cząslkj w układzie K'

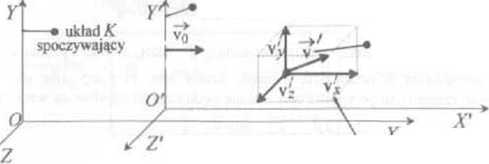
składowa prędkości cząstki w kierunku osiOA'¹

składowe prędkości V = [v_Xłv*v.] w układzie spoczywającym K. dla danej prędkości = l^vx.^y>.^vr] w układzie A" poruszającym się

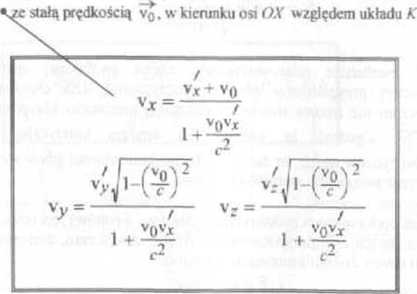
składanie prędkości równoległych ~v' = f\^v.0,0] I

	^V' + V0 ^V = /
	i+^ę
Vo	C^L