skrypt wzory i prawa z objasnieniami68

134

Rozkład Maxwella

■    Prawo Maawdla rozkładu prędkości cząsteczek opisuje rozkład prędkości .-/ąsicczck gazu doskonałego pozostającego w równowadze terroodymmicznej, na którv r.ic dziaują ładne siły zewnętrzne. Rozkład len ustala się w wyniku zderzeń między cząsteczkami w ich bezładnym ruchu cieplnym.

■    Na rysunku po prawej stronic przedstawiono prostokątny układ współrzędnych V; ,v | i v.- (składowe wektora prędkości cząsteczki gazu doskonałego i Prędkości każdej cząsteczki odpowiada punkt na rysunku.

Punkty, które wyobrażają prędkości cząsteczek z przedziału od v do v ł dv, są zawarte między sferami o promieniach v i v + dv Objętość tego obszaru wynosi 4nv²dv Liczbę cząsteczek, których prędkości są zawarte w przedziale (v. v + dv) można przedstawić

jako dA\ = ^vj4itv^,2dv, gdzie fl^y) =    exp|    |. o ,V jesi liczbą

wszystkich cząsteczek. Powyższy wzór można również przedstawić w postaci d.V_v =• \/ tv)dv. Wielkość F\v) =/(v)4nv*jcst funkcją rozkłada prędkości cząsteczek gazu i je.t przedstawiona po prawej stronic Prawdopodobieństwo tego, że prędkość danej

cząs cc/ki jest z przedziału od V do v + dv wynosi d/*v - ~- /’’(v)dv.

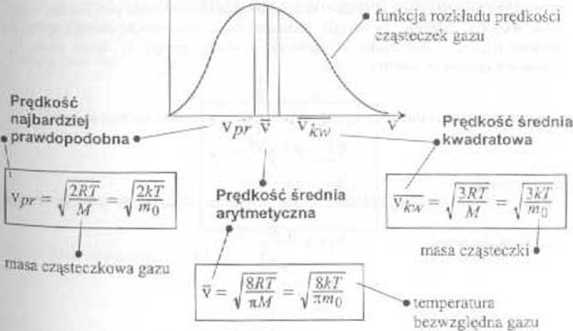
■    Okazuje się, ze każdej temperaturze gazu odpowiada wartość pręckośct cząsteczek v _r, tuka, że prędkością tą t do niej zbliżonymi jest obdarzona największa liczba cząsteczek

• Ir ego prędkość tą nazywany prędkością najbardziej prawdopodobną Można ją wyznaczyć ze wzorów 73 W tym celu należy wykorzystać warunek dla maksimum funkcji £Tv):

r    /"

Rozwiązanie lego równania ma postać

_v , Im

'/» ^c i «o •

■    Korzysiają; z funkcji rozkładu można obliczyć prędkość średnią (prędkość średną arytmetyczną), czyli sumę prędkości wszystkich cząsteczek podzielić przez ich ilość

Wf\v)v dv

ML

i**o

J^ydA\

.V

Średni kwadrat prędkości można natomiast znaleźć z zależności podanej dla kinetycznej teorii guzów £j=^y-^|Af (srr. 132,133), skąd otrzymujemy prędkość średnią kwadratową

u wychodząc z rozkładu prędkości cząsteczek można określić rozkład cnergU kinetycznej mchu postępowego cząsteczek. Podstawiając do wzorów < v-(2Et'mo) ^:'aTXL dv-(2wq£*)"‘ 'd£* otrzymujemy wzór na liczbę cząs*xczck. których energia kinetyczna ruchu postępow ego jest w przedziale od £j do Ł\ - d£

dNs = -jź)    ~^3/2«*P (-

73. Rozkład Maxwella

cząsteczka o prędkości zawartej w przedziale (v. v + dv)

sfera o promieniu v _ _    // ^ j

s*'cni o promieniu v + dv*—    ¹    •/* * • ^#H >

v.<*    * J ^s'y

liczba wszystkich cząsteczek

liczba cząsteczek, których prędkości

są zawarte w przedziale * V* • • od v do vtdv

fdLV_v = NF(\) dv

• masa cząsteczKi gazu

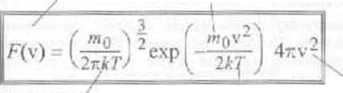
stała Bollzmanna* temperatura bezwzględna gazu cząsteczki 2azu A = 1,38 10 ^J/K

funkcja rozkładu prędkości cząsteczek gazu