skrypt wzory i prawa z objasnieniami06

10

Prędkość

■ Wzór na prędkość w kartezjańskim układzie współrzędnych otrzymujemy w następujący sposób

di di

di

tir

dy

-*•    7,J+di^k =^vr'+^v>y + v,«:

Skorzystaliśmy tutaj z faktu, ze wersory w układzie kartezjańskim nie zależą od czasu czyli

dj_ - dj_ _ d± _ ₀

t// r/f c/r

■ Wzór na prędkość w biegunowym układzie współrzędnych otrzymujemy w następujący sposób:

dr _    \ - dr } . _rd'r

di di^{y 1} di di Pierwszy składnik sumy daje nam wektor prędkości radialnej

v =

dr Cl

Drugi składnik to wektor prędkości transwersalnej /wróćmy uwagę na to. ze pochodna wersora r po czasie —^ jest różna od zera, gdy/ koniec wersora porusza się po okręgu o promieniu równym jeden

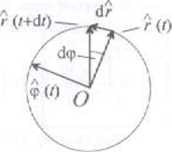
/ rysunku widać, ze wektor dr jest prostopadły do wersora r . czyli kierunek wersora <p Jego wartość równa jest długości luku okręgu czyli

nui

Stąd

|d r| = |r|d<p = <ńp

i wektor prędkości transwersalnej

iii

d /

dtp A

dtp A

'17 «P

[

Kinematyka

2.2 Wektor prędkości w układzie kartezjańskim

11

wektor prędkości czystki ^

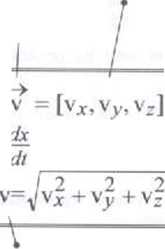
składowe wektora prędkości w- układzie kartezjańskim

v    V -O- u -dl

^x dt ’ y di'^v- di

wartość prędkości (długość wektora prędkości)

2.3 Wektor prędkości w układzie biegunowym

składowa radialna prędkości

V = lv>, V(p]

^V> dt'^VV~^rdi

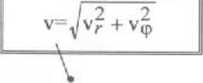
wanosć prędkości cząstki v= v

d(p

wektor prędkości cząstki

dr

składowa transwersalna prędkości