skrypt wzory i prawa z objasnieniami66

130 Potencjały termodynamiczne

■    Rozważania termodynamiki opierają się na wykorzystaniu funkcji stanu, które nazywamy potencjałami termodynamicznymi Zmiany potencjałów w wyniku pewnych przemian s<i równe pracy układu lub otrzymanemu przez układ ciepła.

Przyrost każdego z potencjałów jest różniczką zupełną funkcji, którą jest or. wyrażony. Dla przykładu jednym z potencjałów termodynamicznych jest energia wewnętrzna układu Jej przyrost dlo przemiany odwracalnej ca podstawie pierwszej zasady termodynamiki na postać dU = TdS-pdV. Widać, że w sposób naturalny można wybrać tutaj jako zmienne niezależne entropię ó’ i objętość V Różniczka zupełna funkcji ma żalem postać dU -    J di’4 , J dl'

Otrzymujemy stąd zależności ^ I ^ -T oraz ^    ^ = -p.

funkcji iś-dfJ— T&S’- SdT = 7c1?-;?g F- TdS-Sd7. Stąd dF~ -SdT-pdy.

Wykorzystaliśmy tu zależność na przyrost ÓO Energia swobodna F est zatem funkcją lempcrnmry Ti objętość; V Różniczka zupełna funkcji F[T,V) wyraża sic wzorem

■    I iK-rgią swobodną układu nazywamy funkcję r = U- 7S. Rozważmy różniczkę tej

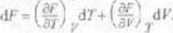
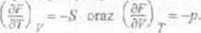
Porównując dwa ostatnie wzory otrzymujemy

Na podstawie pierwszej zasady termodynamiki dlc izotcrmiczncgo procesu odwracalnego można napisać dłf = -dl/TdS - -ÓtU- TS) = -dF. Stąd wniosek, źc praca w izoterm iczr.ym procesie odwracalnym jest równa ubytkowi energii swobodnej ciała.

■    Entalpią układu nazywany funkcję H-V+pT Różniczkując c i uwzględnia a: wzór na di' otrzymujemy dH —AU • pd V+ Edp ~ TdS pdV-*• pd V + I dp - TiLS’ * ¹ er Entalpia jest więc potencjałem termodynamicznym dla zmiennych 5 i p Odpowiednie pochodne cząstkowe wynoszą (|£H = T oraz (^) _v ⁼ *’ •

Jeżeli przemiana zachodzi dla /»**ccnst. to ciepło pobrane pracz układ można przedstawić w postaci dQ=dU+póV*d(U+pV)-=dH Zatem cic|»ło pobrane przez układ w przemianie i zobaryc zn ej jest rów rc przyrost owi entalpii ciała.

■    Termodynamicznym potencjałem Gibbta nazywamy funkcję G H- TS Jej różniczka jest równa dG= Ed^-SdT. Funkcja G jest zatem funkcja ciśnienia p ■ leir.ncraturv T.

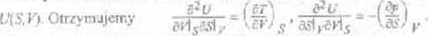
Zakładając ciągłość funkcji U otr/.vmuiemv ieden ze związków Maxwclla (wzory 69.i

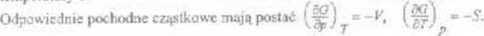
■ Zwią/ki Muc w dla Obliczmy mieszane pochodne cząstkowe rzędu drogiego funkcji

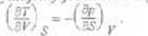
Analogicznie można wyprowadzić pozostałe związki MaxwcJla Są one bardzo przydatne do praktycznego zastosowania zasad termodynamiki.

Termodynamika

131

68. Potencjały termodynamiczne 68.1. Energia swobodna    . _Icmpef3tura

68.2. Entalpia

—m entropia

'

f energia wewnętrzna

/

I// = U+pV¹— -^ob)

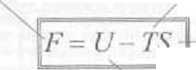
:iśmcrje

68.3. Potencjał termodynamiczny Gibbsa (entalpia swobodna)

y* temperatura

G = H - TS

entropia

entalpia

69. Związki Maxwella

pochodne czas tle o we temperatury po objętości i ciśnieniu przy ustalonej entropii

pochodne cząstkowe entropii po objętości t ciśnieniu przy ustalonej temperaturze

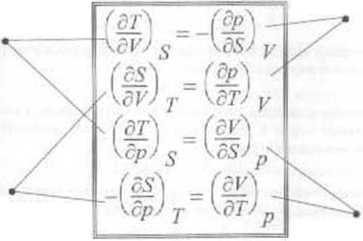
pochodne cząstkowe ciśnienia po entropii i teraperat jrzc przy ustalonej objętości

pochodne cząstkowe objętości po entropii i temperaturze przy ustalonym ciśnieniu