skrypt wzory i prawa z objasnieniami34

66

Ruch środka masy

■    Całkowitą siłę zewnętrzną działającą na układ ciał obliczamy sumując wektorowo wszystkie siły zewnętrzne działające na ciała wchodzące w skład danego układu, niezależnie od tego, czy są one przyłożone w jednym miejscu, czy tez w wielu różnych punktach i do różnych ciał Przez siłę zewnętrzną rozumiemy siłę, której źródłem nie jest inne ciało będące częścią układu.

■    Jeśli początkowo środek masy układu ciał pozostaje w spoczynku i całkowita siła zewnętrzna równa jest zeru. to z II zasady dynamiki przedstawionej w punkcie 29 wynika, żc środek masy pozostanie w spoczynku A więc spowodowanie przemieszczenia jakiegoś ciała wchodzącego w skład układu spowoduje, ze inne ciała w układzie przemieszczą się tak, aby środek masy pozostał w tym samym miejscu Typowym przykładem takiego zjawiska jest przesuwanie się łódki na wodzie podczas przechodzenia z jednego jej końca na drugi koniec.

■    Do opisu ruchu postępowego ciała (ruchu, w którym wszystkie punkty poruszającego się ciała zakreślają te same tory), lub ruchu postępowego układu ciał jako całości, wystarcza znajomość mchu środka masy danego ciała lub układu ciał

■    Bardzo często interesuje nas wzajemny ruch ciał w układzie, który' porusza się jako całość. Przykładem mogą. być drgania atomów w cząsteczce dwnatomowej Wtedy korzystamy z układu środka masy, czyli układu współrzędnych, którego początek pokrywa się z położeniem środka masy układu ciał. W ten sposób "izolujemy" ruch postępowy układu jako całości od ruchów części składowych układu względem siebie

■    Pęd środka masy układu ciał otrzymamy mnożąc całkowitą masę układu i prędkość środka masy Tak wyznaczony pęd jest równy całkowitemu pędowi układu otrzymanemu przez wyznaczenie sumy wektorowej pędów wszystkich ciał znajdujących się w układzie

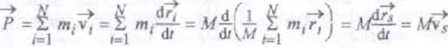
■ Zasadę zachowania pędu dla środka masy układu ciał otrzymamy podstawiając do równania z punktu 29    /*zewn ~ 0 Wtedy = 0 i

otrzymujemy:

M\_s = consi

29. Druga zasada dynamiki Newtona opisująca ruch środka masy ciała lub układu ciał

piędkość środka masy

~    f wektor położenia środka

masy r_s = r,(0

całkowita siła zewnętrzna * działająca na ciało lub układ ciał

przyspieszenie środka masy d/ d/²

masa ciała łub całkowita masa układu ciał

30. Zasada zachowania pędu środka masy układu ciał

/

Dynamika układu punktów materialnych

67

prędkość środka masy układu ciał

P = M\c = const

rn

całkowity pęd jest stały, jeśli całkowita siła zewnętrzna równa jest zeru

całkowity pęd układu będący sumą wektorową pędów ciał tworzących dany układ