skrypt wzory i prawa z objasnieniami57

112 Dynamika relatywistyczna

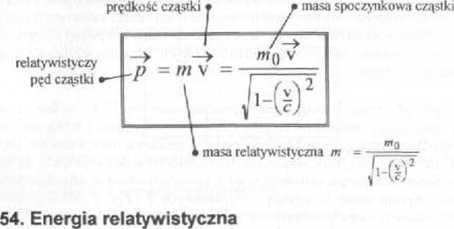
■ Pojęcie masy relatywistycznej wprowadza się po lo, aby posiać zależności pędu od masy i prędkości była w mechanice relatywistycznej taka sama jak w mechanice klasycznej. W niektórych podręcznikach pojęcia tego w ogóle się nie używa, a jako masę rozumie się masę spoczynkową ■ Jeżeli na cząstkę relatywistyczną, tj. taką. której prędkość jest

—►

^ (

- ££. - ii ^wo * ^d'

porównywalna z prędkością światła, działa siła E ( np siła od pola elektrycznego), to powoduje ona zmianę pędu cząstki zgodnie ze wzorem

F =

Powyższa zależność jest uogólnieniem drugiej zasady dynamiki na przypadek relatywistyczny. Bardzo częstym błędem podczas rozwiązywania zagadnień ruchu cząstek pod wpływem sil, gdy prędkości cząstek nie można uważać za dużo mniejszą od prędkości światła, jest stosowanie wzoru klasycznego

F = m a

d v

,'KWc)^{2 d}'

■    W mechanice relatywistycznej cząstce swobodnej oprócz energii kinetycznej przypisujemy energię spoczynkową Dla określenia energii kinetycznej nie można stosować znanego z mechaniki klasycznej wzoru

= Zgodnie ze wzorem na energię kinetyczną w postaci relatywistycznej widać, ze dąży' ona do nieskończoności gdy v-» c , natomiast klasycznie osiągałaby wartość skończoną

■    Masa spoczynkowa niektórych cząstek (np fotonów) jest równa zeru Stąd wynika, ze ich energia spoczynkowa E₀ jest równa zeru. a energia całkowita E, jest równa energii kinetycznej i wynosi

E = cp = mfc². gdzie m_f jest masą relatywistyczną fotonu.

Ponieważ dla fotonu E = hv = h~ , gdzie v jest częstością a X długością fali elektromagnetycznej odpowiadającej fotonowi, mamy

53. Pęd relatywistyczny

54.1 Związek między energią relatywistyczną i pędem

relatywistyczną H i pędem cząstki

i prędkością cząstki