skrypt wzory i prawa z objasnieniami16

30

Ruch ciała po równi

■    Siła występująca w drugiej zasadzie dynamiki jest wypadkową wszystkich sił. które działają na wybrane ciało zc strony innych ciał Czyli stosując drugą zasadę dynamiki należy zastanowić się jakie ciała i jakimi siłami działają na wybrane ciało. Nie wolno mylić takiego określania sił z klasyfikacją sił względem skutków-, które wywołują, tzn wyróżniania takich sił jak siły dośrodkowe, wprawiające w ruch. czy też siły ściągające Siłę można określić względem skutku działania dopiero po rozwiązaniu równań Newtona Wyjaśnia to przedstawiony przykład z równią.

■    Na ciało o masie m znajdujące się na równi pochyłej działa siła grawitacji m~g. którą Ziemia działa na ciało, oraz dwie siły kontaktowe zc strony

równi. Pierwszą z nich jest siła reakcji F_r na siłę nacisku F_n ciała na równię Siła ta jest prostopadła do równi i zgodnie / trzecią zasadą dynamiki, jest

równa co do wartości sile nacisku i przeciwnie do niej skierowana. Poza tym

—>

równia działa na poruszające się ciało siłą tarcia /*'/, styczną do równi i o zwrocie przeciwnym do zwrotu prędkości poruszającego się ciała Wartość siły tarcia jest proporcjonalna do siły' nacisku, F_t - kF_n . gdzie k jest współczynnikiem tarcia (kinetycznego). Suma tych trzech sił, jak to pokazuje

diagram wektorowy, daje nam siłę wypadkową F, która, zgodnie z drugą zasadę dynamiki, powoduje ruch ciała. Siła wypadkowa w tym przypadku jest równoległa do pow-ierzehm równi, a skutkiem jej działania jest zsuwanie się ciała. Możnaby więc nazwać tę siłę siłą zsuwającą

■    Przy- praktycznym rozwiązywaniu zagadnienia ruchu ciała po równi pochyłej, korzystamy z oczywistego taktu, że nich może zachodzić jedynie wzdłuż równi W naturalny sposób sprowadza to wektorowe równanie /■ = m~a ( równoważne trzem równaniom skalarnym - patrz punkt 8.1) do jednego równania skalarnego, jeśli za kierunek osi współrzędnej przyjmiemy kierunek wzdłuż równi. Zwrot wybierany tak. aby przyspieszenie ciała było dodatnie.

■ Na pierwszym rysunku pokazano również siły, którymi zgodnie z trzecią zasadą dynamiki zsuwające się ciało działa na równię. Są to siła nacisku F_n

i siłę tarcia Ft = -Ft Należy pamiętać także o tym, że zgodnie z trzecią zasadą dynamiki, zsuwające się ciało działa na całą Ziemię siłą równą -mg

9. Równia pochyła

przyspieszenie ciała

siła nacisku ciała na równię

siła tarcia działająca na zsuwające się ciało

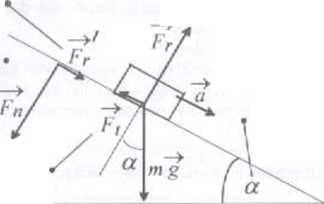
kąt nachylenia równi do poziomu

sila tarem działająca na równic

/siła reakcji równi na siłę nacisku

—> /
F	A
F	—
	F,
siła wypadkowa
działająca na ciało	->
powodująca jego	"■ F
zsuwanie się z równi

mg

m a

siła ciężkości, którą Ziemia działa na zsuwające się ciało

F =

siła reakcji równi na nacisk ciała równa co do wartości składowej siły ciężkości prostopadłej do równi Fr - F_n mg cos a

siła tarcia proporcjonalna do siły nacisku

F/ kFn - kmg cos a

ma = mg sina - kmg cos a

przyspieszenie zsuwającego ³>? (wzdłuż równi) ciała • składowa siły ciężkości na kierunek wzdłuż równi