skrypt wzory i prawa z objasnieniami13

24

Ruch po okręgu

■ Ruch fx> okręgu jest szczególnym przypadkiem płaskiego ruchu krzywoliniowego. Niech promień okręgu wynosi r. Położenie punktu na okręgu można jednoznacznie określić podając kąt <p zakreślony przez promień wodzący Ruch ciała jest określony przez funkcję o = <p(/) Jeżeli przez s oznaczymy drogę przebytą przez ciało po okręgu w czasie, w którym droga kątowa wynosiła cp. to zachodzi związek

s = tpr.

Różniczkując obie strony tego związku względem czasu otrzymujemy

śl -

di dt

Wielkość ds/dt jest prędkością liniową v ciała w ruchu po okręgu a </<pIdi nazywamy prędkością kątową i oznaczamy symbolem ca. Zatem mamy zależność    v = tor

Różniczkując obie strony tej zależności względem czasu otrzymujemy

d\ _ dlii _r di dt

Wielkość d\'>dt jest przyspieszeniem stycznym a_x a Jco'dt przyspieszeniem kątowym c. Mamy zatem    a-, = er.

W ruchu po okręgu przyspieszenie normalne nazywamy przyspieszeniem dośrodkowym gdy ż jest skierowane do Środka okręgu Wynosi ono

Qn - ud ⁼ T ~ ^<0“^r-

Jak widać ruch punktu materialnego poruszającego się po okręgu o promieniu r można opisać podając jego wielkości kątowe o.co.e lub wielkości liniowej, v,a$

Prędkość kątowa i przyspieszenie kątowe są wielkościami wektorowymi,

%

(0

których kierunki są równoległe do siebie i prostopadłe do płaszczyzny okręgu Zwrot wektor <i> jest wyznaczony zgodnie z regułą śruby prawoskrętnej - zwrot wektora <o pokrywa się z kierunkiem ruchu postępowego śruby prawoskrętnej, która obraca się zgodnie z

kierunkiem ruchu punktu po okręgu.

Wektor przyspieszenia kątowego e ma zwrot zgodny ze zwrotem wektora tu w przypadku przyspieszonego ruchu po okręgu fe •= —■ > 0) i przeciwny - w przypadku ruchu opóźnionego (e = ~ < 0)

7. Ruch po okręgu 7.1 Prędkość kątowa

prędkość kątowa ciała j kąt zakreślony przez promień wodzący \    t w czasie <1/

f/ip

Kinematyka

25

wartość prędkości liniowej ciała poruszającego ssę po okręgu o

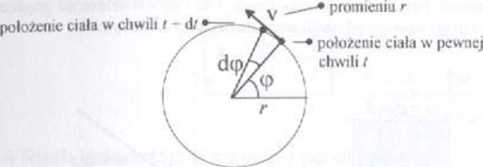
V = co r 4-V—

prędkość liniowa A ciała poruszającgo się po okręgu

7.2 Przyspieszenie kątowe

przyspieszenie kątowe ciała

—• promień okręgu prędkość kątowa ruchu ciała

„ _ do _ d²<P

di d,²

przyspieszenie w ruchu ♦ po okręgu

a =a_s +aj as = e r a_d = co²r

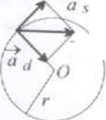
i dośrodkowego a j

■* rozkład wektora przyspieszenia całkowitego a na wektor

>

a \ przyspieszenia stycznego a s