skrypt wzory i prawa z objasnieniami11

20 Rzut poziomy ■ Rzut poziomy w polu siły ciężkości może być rozpatrywany jako ruch złożony z dwóch niezależnych ruchów: ruchu ciała z prędkością stała w kierunku poziomym i ruchu jednostajnie przyspieszonego w kierunku pionowym (spadku swobodnego) z przyspieszeniem g. Wprowad/my kartezjański układ współrzędnych w taki sposób, aby wektor g był skierowany przeciwnie niż oś OY, a prędkość v ₀ była skierowana zgodnie z osią OX Ruch wzdłuz osi OA jesl to ruch jednostajny ze stałą prędkością, a wiec

v* = v₀ i x=v₀/.

W kierunku osi OY mamy spadek swobodny z prędkością

^v> =

a współrzędna położenia ciała na osi O* zależy od czasu zgodnie z zależnością:

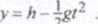
Jeżeli wyeliminujemy z równań jc = jr</) i >•=></)czas t otrzymamy równanie toru

Jest to równanie paraboli.

■ Wartość prędkości v w rzucie poziomym w dowolnej chwili t wynosi

■ Obliczmy wartości przyspieszenia stycznego a* i przyspieszenia normalnego a_n Zgodnie z definicją mamy

al + a²n = g². czyli

Przyspieszenie normalne można wyznaczyć wykorzystując związek

Z kolei korzystając z definicji przyspieszenia normalnego a„ - można wyznaczyć zależność promienia krzywizny toru R od czasu

współrzędne r/uconcgo poziomo    składowe wektora prędkości 7

całkowitego (przyspieszenie ziemskie} na wektory przyspieszenia stycznego i normalnego'do toru ruchu

	r =
zasięg rzutu •
czas trwania rzutu •--	- ‘()A »