skrypt wzory i prawa z objasnieniami03

4

Układy współrzędnych

■ Układem odniesienia nazywamy ciało, względem którego rozpatruje się ruch punktu materialnego (czystki) Z układem odniesienia można związać układ współrzędnych, dzięki czemu położenie każdego poruszającego się punktu względem układu odniesienia można jednoznacznie określić za pomocą trzech współrzędnych (dla ruchu w przestrzeni), dwóch współrzędnych (dla ruchu w płaszczyźnie) luh jednej współrzędnej (dla ruchu po zadanej linii).

■ W zadaniach najczęściej mamy do czynienia z ruchem prostoliniowym i ruchem płaskim Stosujemy wtedy układy współrzędnych kartezjański jedno-i dwuwymiarowy oraz układ biegunowy W przypadku ruchu trójwymiarowego stosujemy układy współrzędnych kartezjaóski trójwymiarowy, cylindryczny (walcowy) i sferyczny (kulisty).

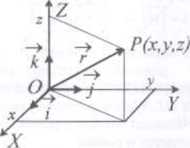
■ Wektorem położenia lub promieniem wodzącym danej cząstki nazywamy wektor łączący początek układu współrzędnych z punktem, w którym znajduje się cząstka.

■ W układzie kartezjańskim rzuty wektora położenia na osie układu współrzędnych są równe współrzędnym punktu, w którym znajduje się cząstka

r - r_x i + ryj + r_: k =x i + yj + zk Wektory' jednostkowe, czyli wersory (wektory o długości równej 1), są w tym przypadku skierowane zgodnie ze zwrotem osi współrzędnych, mają wiec stały

kierunek w przestrzeni. Oznacza się je najczęściej symbolami i, j , k, ale czasami również x,y,z.

Długość wektora położenia w kartezjańskim układzie współrzędnych wynosi

r=|7| = ^+>²-i^J

■ W układzie biegunowym współrzędnymi punktu P, w którym znajduje się cząstka są r - odległość punktu od początku układu O oraz kąt o między prostą przechodzącą przez punkty O i P a przechodzącą przez początek układu prostą zwaną osią biegunową W'ektor położenia cząstki zadany jest wzorem podanym w punkcie ł 2 Natomiast wektory prędkości, przy spieszenia (czy też dowolny inny wektor) zapisujemy w postaci

4 ^A 4 ^A

A - Ar ^ +/J <p <p

gdzie A_r i /tę są rzutami wektora A na kierunki wyznaczone przez wersory r i

<p związane z położeniem punktu P. Wersor V leży na prostej OP a wersor $

jest prostopadły do niego i zwTócony w stronę wzrostu kąta <j> Długość —►

wektora A w układzie biegunowym wynosi

Kinematyka 5

1. Wektor położenia (promień wodzący)

1.1 Wektor położenia we współrzędnych kartezjańskich

wektor położenia f punktu materialnego

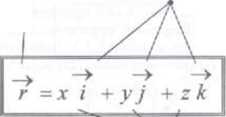
wektory jednostkowe (wersory) w kierunku osi OX. OY. OZ

m-m-m ■

współrzędne wektora położenia w układzie kartezjańskim

1.2 Wektor położenia we współrzędnych biegunowych

wektor położenia dla danego punktu materialnego

wektor jednostkow y (wersor) dla danego wektora położenia |r| = 1

= reosep = rsin<p

*^/\vzory przejścia ze współrzędnych biegunowych r. <p do kartezjańskich x.y

• wzory przejścia ze współrzędnych kartezjańskich x. y do biegunowych r. <p

t l

r=

<? = aretan -

oś OX pokrywająca się z osią biegunową