skrypt wzory i prawa z objasnieniami05

8

Prędkość

■ Tor jest to krzywa opisywana w przestrzeni przez poruszający się punkt W zależności od kształtu toru rozróżnia się prostoliniowy i krzywoliniowy ruch punktu Ruch punktu nazy wa się płaski, gdy wszystkie odcinki jego toru lezą w jednej płaszczyźnie

■ Równanie toru we współrzędnych kartezjanskich ma ogólną postać <D(x.^,z) = 0.

np. dla ruchu po okręgu o promieniu R i środku w początku układu współrzędnych równanie toru jest następujące:

*²V = *² .

czyli

<${x,y,z)=x² +y² - R² = 0 .

■    Prędkość (prędkość chwilowa) jest to wielkość wektorowa v równa pierwszej pochodnej wektora położenia r poruszającego się punktu względem czasu t.

Z definicji prędkości wynika, źe

d^,

zatem wektor prędkości jest skierowany zawsze wzdłuż stycznej do toru w kierunku ruchu punktu

■    Długość drogi s jest to suma wszystkich odcinków toru, przebytych przez punkt w rozpatrywanym przedziale czasu <7^,/#)

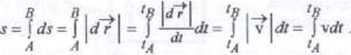
■ Zauważmy, że jeśli ciało porusza się po torze ze stałą prękością v, to prędkość średnia równa jest tej prędkości i zachodzi związek

v,= v=f,

gdzie s jest drogą przebytą przez ciało w^r czasie t.

Kinematyka 9

2. Prędkość

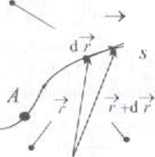
wektor prędkości

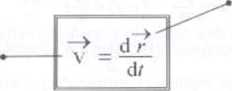
wektor położenia cząstki r *= r U)

elementarne przesuniecie d r = x dl |d? ^

d' - droga przebyta przez cząstkę od chwili .* do chwili f +- d/

wektor położenia cząstki q w chwili i

początek układu współrzędnych *

J prędkość cząstki w chwili / y    tor ruchu cząstki

B wektor położenia cząstki w chwili {+ d/

droga przebyta przez cząstkę w przedziale czasu {t4-'<{>

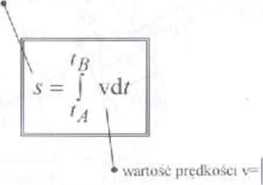
d?

d /    dl

2.1 Prędkość średnia

droga przebyta przez cząstkę od chwili / .| do chwili ty

prędkość średnia poruszającej się cząstki w przedziale czasu (t j_T 1 r_{)