skrypt wzory i prawa z objasnieniami22

42

Pole grawitacyjne

■ Jeśli w przestrzeni umieścimy pewną masę M (źródło pola grawitacyjnego), to wprowadzając w dowolne miejsce tej przestrzeni inną masę tu, stwierdzimy, że na wprowadzoną masę będzie działać siłą przyciągania o wartości opisanej prawem grawitacji Newtona:

F- .

skierowana do /ródla pola grawitacyjnego. Przypomnijmy, że powyższy wzór jest prawdziwy dla mas punktowych i mas kulistosymetrycznych. W tym drugim przypadku położenie masy identyfikujemy ze środkiem kuli. Oczywiście zgodnie z III zasadą dynamiki Newtona i masa m działa na masę M. Jednakże przy założeniu, że m «M , zmiana położenia źródła poła pod wpływem tej siły jest pomijalnie mała

4?(t)dZ=f(-o

■ Siła grawitacji powodując ruch ciała z punktu A do punktu B wykona pracę, którą wyznaczamy korzystając z definicji pracy

4*8 IW

Licząc powyższą całkę zauważmy że iloczyn skalamy r d r można wyliczyć rozkładając elementarną zmianę wektora położenia na składową równoległą do wektora położenia i na składową do niego prostopadłą, czyli otrzymamy r d * = r i dz * + dry J = r drp = | ~r | | dr\\ = rdz.

Stąd wartość całki wyniesie

«A,B= ~ GmM f * - GMm(± - Jj)

A

Zauważmy, że otrzymany rezultat nie zależy od drogi po jakiej przechodzimy od punktu A do punktu B. a tylko od początkowej r_A i końcowej r_H odległości przemieszczanego ciała od źródła pola Jeśli r_A =r# , to praca równa jest zeru (praca po drodze zamkniętej) Dzięki tym własnościom pole grawitacyjne jest polem zachowawczym (patrz punkt 21).

■    Powyżej wyliczono pracę sił pola Często w zadaniach jest mowa o pracy jaką wykonuje siła równoważąca siłę pola. A więc siła, jaką musimy podziałać, aby przesunąć ciało w polu grawitacyjnym. Praca tej siły będzie miała przeciwny znak niż praca siły pola (patrz komentarz do punktu 13 1)

■    Wzory' znajdujące się w punktach 16 i 16. ł dotyczą poła grawitacyjnego wytworzonego przez jedno ciało W przypadku poła. którego źródłem jest więcej ciał rozmieszczonych w zadany sposób w przestrzeni stosujemy zasadę superpozycji pól Tzn. sumujemy (oczywiście wektorowo) siły pochodzące od poszczególnych ciał.

16. Pole grawitacyjne

Dynamika punktu materialnego

43

—►

ciało o masie    • siła grawitacji działająca

będące źródłem    na ciało o masie m

pola grawitacyjnego (AY » m)

F		^ Kim ~r ^J -- r^2 r
stała grawitacji'			^ odległość masy m od środka

źródła pola grawitacyjnego

16.1 Praca sił pola grawitacyjnego

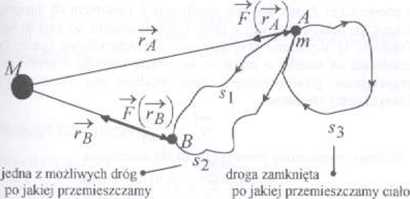
ciało z punktu A do łi    z punktu A do A

(praca w tym przypadku jest równa zem)

Ki~>b

odległość punktu łi od źródła pola

odległość punktu A od źródła pola

praca wykonana przez

^ły grawitacji przy przemieszczaniu

wała z punktuj do B po drodze