skrypt wzory i prawa z objasnieniami07

12

Przyspieszenie

■    Przyspieszenie (przyspieszenie chwilowe) a jest to wielkość wektorowa, charakteryzująca szybkość zmiany prędkości poruszającego się punktu, równa pierwszej pochodnej wektora prędkości względem czasu

■    W układzie kartezjańskim wzór na przyspieszenie otrzymujemy w następujący sposób

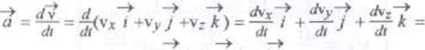
= a x i + ay j + a z k

■ Zgodnie z drugą zasadą dynamiki (patrz punkt 8 l) przyspieszenie poruszającej się cząstki równe jest

gdzie F jest wypadkową siłą działającą na cząstkę a m masą cząstki równanie

Stąd

di²

możemy traktować jako różniczkowe równanie ruchu cząstki.

Kinematyka

13

3. Przyspieszenie

wektor przyspieszenia cząstki

^ wektor prędkości p wektor położenia

pochodna wektora prędkości po czasie r

druga pochodna wektora położenia po czasie \

3.1. Przyspieszenie w układzie kartezjańskim

wektor

przyspieszenia f

dv

d/

składowe wektora przyspieszenia w układzie kartegańskim

a = [a_x, a_y. a₌] dv,, d²v

_x _q-x    - ^^v- _ d^z-

d/² ' -^V d/ d,² ’ ² " d, “ _d/2

/ 2 2 2

CI — yi Q_x

wartość przyspieszenia