skrypt wzory i prawa z objasnieniami08

14

Przyspieszenie

■ Wzór na przyspieszenie w biegunowym układzie współrzędnych otrzymujemy w następujący sposób:

-►    di *    dv_r a    a    do

^a    * "£l^{Vr r}*^v"    ⁼ 1T ^{r + v}'* ⁺-dT * ⁺ v*~óF

a. i/	do A	. A , d ip w A
dr	^= d?* *	<U ' di ^r

Pochodne wersorów po czasie wyznaczamy podobnie jak w komentarzu do punktu 2.3 otrzymując:

Uwzględniając powyższe zależności i wyrażenie na prędkość radialna i transwersalną (patrz punkt 2 3) otrzymujemy przyspieszenie w układzie biegunowym jako sumę wektorów przyspieszenia radialnego i transwersalnego

—r    A

a = a<p tp + Ur r

—►    A    A

«J(p +■ Of

■ Wyznaczmy wektor przyspieszenia w taki sposób, aby wyodrębnić część przyspieszenia związaną ze zmianą wartości prędkości i część związaną ze zmianą kierunku wektora prędkości. W' tym celu wprowadza się wersor s jako wektor jednostkowy mający kierunek i zwrot wektora prędkości cząstki (czyli kierunek styczny do toru). Wtenczas można zapisać

-* A

i stad

dv_₌ dv£    d_>

di d /    di

Widać juz, że pierwszy składnik powyższej sumy to będzie składowa przyspieszenia styczna do toru. związana ze zmianą wartości prędkości, natomiast drugi składnik będzie związany ze zmianą kierunku ruchu Zmianę wers ora s w czasie możemy wyznaczyć następująco

d£₌ dVd_v.dJ

dr <1» di di

W'ielkość di jest drogą przebytą przez cząstkę w czasie dr. Drogę tę możemy traktować jako drogę po obwodzie stycznego do toru okręgu o promieniu R (R - promień krzywizny toru), czyli d.v = Rd«r> (ckp jest kątem jaki zakreśli promień R w czasie dr) Stąd

d£ I £s _ i £ d* R dq» ~ R '

u,v i- a*

di ^S + R ”

gdzie « jest wersorem prostopadłym do s i mającym zwrot do środka okręgu (.patrz komentarz do punktu 2.3). Tak więc składowa przyspieszenia związana ze zmianą kierunku ruchu ma kierunek normalny do toru (prostopadły do stycznej do toru) i stąd nazywa się wektorem przyspieszenia normalnego Ostatecznie rozkład wektora przyspieszenia na wektor przyspieszenia stycznego i wektor przyspieszenia normalnego ma postać —► dv £ , a

3.2 Przyspieszenie w układzie biegunowym

wartość przyspieszenia w układzie biegunowym

wektor przyspieszenia cząstki

- -y    }    j

a = [a_r*a<p]. a = Jap

_ar=Ą__r(^.)²

składowa radialna wektora przyspieszenia

składowa transwersalna ' wektora przyspieszenia

Kinematyka

15

dr²    ^d/>

„ -dr d<p . d²ip Idf.^dp''²

‘P "dr dr    rdrV di)

3.4 Przyspieszenie styczne i normalne

tor ruchu cząstki

wektor przyspieszenia normalnego

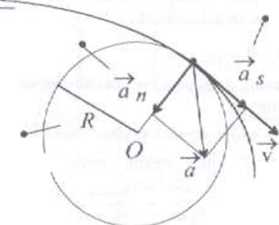
^ wektor prędkości cząstki

promień krzywizny toru (promień okręgu i stycznego dolom) '

wektor przyspieszenia stycznego

a = a • + a

składowa

styczna

przyspieszenia

wektor przyspieszeiua całkowitego, 7

—>

składowa normalna

przyspieszenia *-

wartość przyspieszenia całkowitego