skrypt wzory i prawa z objasnieniami61

120

Gaz doskonały. Równanie van der Waałsa

■    Ca/ doskonal} definiuje się następująco:

* cząsteczk’ gaza poruszają się chaotycznie we wszystkich kierunkach, z których żaden nie jest uprzywilejowany,

-    cząsteczki zderzają się sprężyście ze sobą wzajemnie i ze ściankami naczynia, w którym znajduje się gaz,

-    między cząsteczkami nic działają żadne siły, poza krótką chwilą, w której następuje zderzenie,

-    cząsteczki poruszają się od zderzenia do zderzenia ruchem jednostajnym

prostoliniowym,

-    suma objętości cząsteczek gazu jest dużo mniejsza od objętości naczynia, w

który r.i znajduje się gaz.

Każdy gaz rzeczywisty pod odpowiednio małym ciśnieniem (dostatecznie . zfzedzcny; ma własności zbliżone do gazu doskonałego.

■    Star. danej masy gazu jest określony przez wartości trzech parametrów C1ŚII.C1U3 p, objętości 1 i temperatury T. Związek między tymi parametrami nu>zx

yc dany w postaci równania Ftp, V,T)~ 0. które nazywamy równaniem stanu. Da gazu doskonałego równanie stanu (równanie C Iapeyrona) ma postać pi' = >;RT , gdzie n esl liczbą moli gazu. a /? stałą gazową. Dla stałej masy gazu równanie *.o mniemy zapisać w postaci pi'!T =const Wprowadzając wielkość ( - ił \'_A, która jest nazywana stałą Uoltzmanna. a V* = 6,022 • I0²³ mol ¹ jest lic/ ą cząsteczek w jednym molu gazu (liczba Avogadro), możemy przekształcić równanie Clupcyrons do postaci

^1=    . nS_ĄkT= V kT,

gdzie .V est całkowitą liczbą cząsteczek gazu.

■    W warunkach normalnych (7’_::    273AT 0°C, pg - 1.10 lD⁵ l’a) olęętuśi I

mola każdego gazu jest State i wynosi

l'o * ifV^,ra ^Ł ?2.4 1/moi - 22,4 10"³ m^:Vmnl

■    Wraz ze wzrostem ciśnienia i ze spadkiem temperatury obserwuje się dla gazu rzeczywistego odstępstwa od równania stanu gazu doskonałego. Wzrost gęstości gazu powozu je. źe dużą rolę zaczyna odgrywać objętość cząsteczek oraz oddzlaływanin międzycząstcczkowc.

Zachowanie s:ę gazów rzeczywistych w szerokim zakresie gęstości opisuje równanie Van der Waałsa. Otrzymuje się je przez wprowadzenie dwóch poprawek do rów nania stanu gazu doskonałego (pV - nRT)

Poprawka /rai* charakteryzuje dodatek do ciśnienia zewnętrznego, który wyn ka ze wzajemnego przyciągania się cząsteczek gazu. Gaz wywiera n:i ścianki naczynia ciśnienie/», które jest równe ciśnieniu wywieranemu na gaz z zewnątrz Z :u>\yodu przyciągania się cząsteczek gaz jest jakby ściskany ciśnieniem większym od p.

Ponieważ cząsteczki mają skończoną objętość, w ięc przestrzeń dostępna d'a mchu cząsteczek jest w rzeczywistości mm cisza od objętości naczynia V. Poprawka nb charakteryzuje tę część objętości, która me jest dostępna dla ruchu cząsteczek

Termodynamika 121

61. Równanie stanu gazu doskonałego (Równanie Clapeyrona)

* masa gazu /

-4-

liczba moli

T

, liczba wszystkich cząsteczek gazu

cisnicnic gazu doskonałego

\T=—”^-1    ¹

\pV=n RTL

\ /    > I • tempei

•liczba Avogadro masa molowa gazu

raiura gazu doskonałego

objętość gazu« doskonałego

• stała gazowa R - 8,31

moMĆ

R = kNi

*•    •liczi

stała Boltzmanna *    liczba Avogadro

* = 1-³⁸' I0^_23J/K    _Są = 6 022 • I0²³mol^{_ 1}

61.1 Równanie stanu dla stałej masy gazu

stała wartość dla danej masy gazu doskonałego

\

parametry stanu gazu doskonałego na początku procesu termodynamicznego

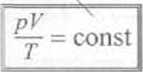
62. Równanie Van der Waałsa

P\V\ _P2^V1 T\ T₂\

parametry stanu gazu doskonałego na końcu procesu termodynamicznego

stałe Van der Waałsa Jt (wyznaczone doświadczalnie)

ciśnienie wywierane przez gaz na ścianki naczynia

mol-K