skrypt wzory i prawa z objasnieniami62

122 Przemiany stanu gazu doskonałego

■    W trakcie przemiany i/obaryc/ncj spełniony jest warunek p const,a więc _r równania stanu gazu doskonałego wynika zależność Y tT=const lub ry7*i = y^tTi (prawo Gay - Lussaca)

W cza>:c przemiany izobaryczncj gaz pobiera ciepło i wykonuje pracę Ilość ciepła potrzebna do ogrzania n moli gazu od temperatury Tdo temperatury T * aT w przemianie izobaryczncj wyraża się wzorem

Q — nCpAT,

gdzie zakładamy, że C_p - ciepło molowe pod stałym ciśnieniem jest stałe.

Praca W wykonana przez gaz w przemianie izobaryczncj wyraża się wzorem

'?    ^yf

W= pĆV=-p | d v = y₂ - V, )=p&r .

«-^:l    ‘'i

Pierwsza zasada termodynamiki dla tej przemiany ma więc postać nCp£s.T = A U~rpAV.

■    Przemiana i/.ucbnryczna gazu doskonałego zachodzi przy w-arunku I const, który jest równoważny warunkow i p!T- const lub p-JT\ ~P2'^2 (pniwn Charicsa)

W czasie przemiany izochoryczncj gaz nic wykonuje pracy dff^/= pdV- 0.

Ilość ciepła potrzebna do ogrzania n moli gazu od temperatury T do temperatury T + A T wynosi Q - nCyAT* gdzie Cy jest ciepłem molowym przy stałej objętości P.erwsza zasada termodynamiki dla lej przemiany ma więc postać

nCyAT - AU.

■    Powyższy wzór w postaci różniczkowej diz = nCy&T wyraża zmianę energii wewnętrznej r. moli gazu przy zmianie temperatury o dT w dowolnym procesie termodynamicznym.

■    Równanie Mayera. Zastosujmy pierwszy zasadę termodynamiki do przemiany izobaryczncj n moli gazu doskonałego

nC_pAT= AU-^pAY.

Ponieważ dla gazu doskonałego mamy A U = nC j/AT, więc otrzymujemy nC_pAT =nCyAT+pAV 7. równania Clapeyrona mamy pAY = nRAT Zatem nCpAT-HRAT^nCytsT,

skąd dzieląc obie strony równania przez nAT otrzymujemy

Cp ~ Cy — R.

Dla każdego gazu ciepło molowe pod stałym ciśnieniem jest zawsze większe od ciepła molowego w stałej objętości o wielkość równą stałej gazowej Równanie Mayera można także zapisać dla cicpeł właściwych

gdzie M jest masą cząsteczkową gazu

63. Przemiany stanu gazu doskonałego

63.1- Przemiana izobaryczna

objętość gazu doskonałego

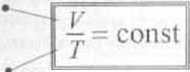
P^A

temperatura bezwzględna gazu doskonałego

ciepło molowe

ciepło pobrane przez gaz    przy stałym ciśnieniu

w czasie przemiany izobaryczncj

izobara / (^-consi)

pip]

w

■

^rTTvi

v

liczba mol gazu

Q = n CpAT= m CpAT

x

li gazu *    /

masa gazu •

praca w przemianie izobaryczncj

ciepło właściwe przy stałym ciśnieniu

63.2. Przemiana izochoryczna

ciśnienie gazu doskonałego

ly = const

izochoru (V - const i

/

siała w artość dla danej masy gazu doskonałego

ciepło pobrane przez gaz w czasie przemiany izochoryczr.cj

\0 = n CyAT = m c yAT

ciepło molowe

przy stałej objętości •

Równanie Mayera

■ ciepło molowe przy stałym ciśnieniu <

»stała gazowa J

o.-K

i zmiana

temperatury gazu

ciepło właściwe przy stałej objętości

/

/    .» stała gazów?

/"■ = 8.

C p — L y = K |    rao

wielkość zależna od ilości atomów w cząsteczce ga?.i

_l

• ciepło molowe przy stałej objętości

/

Cy '

¥-