skrypt wzory i prawa z objasnieniami69

136

Rozkład Boltzmanna

T

■    Ko/Mud Boit/iminua akrcśla slon układu cząsteczek gazu poruszających atą chaotycznym ruchem cieplnym w obecności dowolnego potencjalnego polo sił, np. pola sił ciężkości. Rozkład ten porwała obliczyć liczbą cząsteczek w funkcji ich energii po'.cncj.iir.ej.

Rozkirtć MojcwcJIb dotyczy prędkości cząsteczek a zatem ich energii kinetycznej, natomiast rozkład Boltzmunna dotyczy ich energii potencjalnej

■    Rozkład cząsteczek w polu siły ciężkości Przykładem rozkładu Boltzmamui jehi rozkład cząsteczek wchodzących w skład atmosfery ziemskiej. Gdyby mc było chaotycznych ruchów cieplnych, wszystkie cząsteczki powietrza opadłyby pod działaniem siły ciężkości na powierzchnię Ziemi. Z drugiej zaś strony, gdyby nic było siły ciężkości, wszystkie cząsteczki rozłożone byłyby równomiernie w przestrzeń;, ponieważ w nieobecności sił zewnętrznych taki rozkład jest najbardziej prawdopodobny. W rzeczywistości istnieje ; siła ciężkości i ruch cieplny. Rozkład cząsteczek będzie zatem nierównomierny. W oparciu o prawo rozkładu Boltzmanna (wzór 74), zakładając T = const, otrzymujemy wzór na koncentracją cząsteczek n_ti na wysokości h.

«_A*aoe*p(-^).

gdzie »_u jest koncentracją cząsteczek na wysokości h - 0, a tn masą cząsteczki Jak widać liczba cząsteczek w jednostce objętości maleje wykładniczo w polu siły ciężkości ze wzrostem wysokości h

■    Wzór barometryczny okrrśln zmiano ciśnienia atmosferycznego ze wzrostem wysokości. Zakładając 7*= const, z równaniu Clipcyrona w postaci pV- .V kT, otrzymujemy koncentrację cząsteczek (liczbę cząsteczek w jednostce objętości) na wysokości h = 0 oraz !\ no = ptfkT oraz n/, =pi,łkT. Podstawiając le zależności do wzoru r.o rozkład cząsteczek w polu siły ciężkości otrzymujemy

/>*®p₀exp(-3&) =/»0«p(-^£).

gdzie />o oznacza ciśnienie na wysokość: h - 0 a M jest średnią masą cząsteczkową powietrza {obliczoną na podstawie zawartości azotu, tlenu i innych gazów w powietrzu).

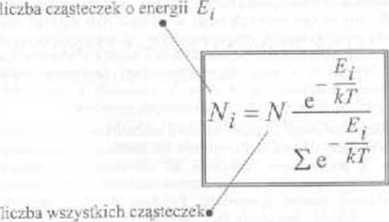
■    W rozkładzie Boltzmanna {wzór 74.' energia cząsteczki E może przyjmować ciągły zbiór wartości. Załóżmy, ze energia cząsteczki może przyjmować jedynie dyskretne wartości £) ,£3, —- Jeśli mamy A^f cząsteczek, to wtedy energię E_i będzie miało .V₍ cząsteczek zgodnie ze wzorem

_5l

NfAc w.

gdzie A jest współczynnikiem proporcjonalności, który powinien spełniać równanie I,V, = d lc*r*N.

A

Stąd otrzymujemy    A=Sf Ic W

Zatem wzór na rozkład Boltzmanna dia przypadku dyskrcmych wartości energii

74. Rozkład Boltzmanna

koncentracja cząsteczek w punkcie, w którym energia a cząsteczki ma wartość E \

Termodynamika 137

ę różnica energii

M

|«£ = «0^e *^r\

koncentracja cząsteczek w punkcie, w którym energia cząsteczki ma wartość £p

74.1. Wzór barometryczny

ciśnienie atmosferyczne a. na wysokości h

ÓJ-=E- e.

o

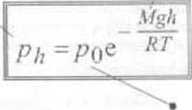
»temperatura bezwzględna cząsteczek

^ siała Boltzmanna

**= 1,38-10"²³!*

średnia masa

/cząsteczkowa powietrza A/g/i

ciśnienie atmosferyczne na wysokości ń “ ó (na poziomic morza)

74.2. Rozkład Boltzmanna dla skończonej liczby stanów energetycznych

cząsteczek ma postać

_<V_/=/V

C »r

£,

le tr